Bundling Information Goods:
Pricing, Profits and Efficiency
Yannis Bakos* and Erik Brynjolfsson**
Appendix 1: Proofs of Propositions
Proposition 1
Proposition 2
Proposition 3
Proposition 4
Proposition 5
Proposition 6
Appendix 2: A mechanism for recovering information about the valuations of individual goods
Consider a bundle of zero marginal cost goods, each with
i.i.d. valuations with mean
and standard deviation
. Let
be the probability density function for
a consumer's valuation for this bundle, and let
and
be the mean and standard deviation for the valuation of the bundle
adjusted for n; i.e.,
and
. Denote
by
,
the optimal mean price for the
bundle (adjusted for n) and the corresponding quantity (
),
and let
be the resulting profits per good
.
Let
and
. We show that
and
. (If these limits do not exist, the same
reasoning can be applied to convergent subsequences of
and
, as
is bounded, and so is
because of the finite variance assumption.)
If P>m, there
exists some e>0 such
that for all large enough n, . By the weak law of large
numbers,
, where
or
. Thus if P>m,
, and since
is
bounded,
, which contradicts the optimality of
and
.
If P<m, there exists some e>0 such that for all large enough n, . Let
, and
the corresponding quantity. The weak law
of large numbers implies that
, and
.
Since for large enough n,
, it follows that
, which again contradicts the optimality of
and
. Thus
.
If , let
and
, so that
. Since
converges to Q and
, there exists some
such that
for all
.
Choose
such that
, which is satisfied for
, and let
be the quantity sold at price
. By the weak law of large numbers,
, and thus
there exists some
such that
for all
. Finally, since
converges to m as shown above, there exists some
such that
for
. Let
. Then for
, setting a price
yields corresponding sales
and revenues
. Since e was chosen so that
, we get
,
contradicting the optimality of
and
.
Using the same notation as in Proposition 1, we assume that, for all integer and all
,
.
This assumption implies that the quantity of the bundle of
goods sold at price
per good will increase compared to the bundle
of
goods, i.e.,
. This guarantees that
. Adding the
th good to the bundle is desirable
for the seller, because a bundle of
goods is more profitable than
a bundle of
goods plus a single good sold separately,
since
.
Assumption A5 also implies that (otherwise
would not be optimal), allowing the reasoning above to be applied
inductively, which proves the proposition for all
.
If the marginal cost is higher than the mean valuation, it is easily seen that bundling
is unprofitable at the limit as . Separate sales are still
profitable as long as some consumers' valuations are higher than the marginal cost.
Without bundling, the seller faces a downward sloping demand function for each individual good, resulting in a monopolistic equilibrium
price of
and corresponding profit of
.
Bundling allows the seller to capture the entire consumer valuations, thus resulting in
average profit
. Bundling becomes unattractive when
, or
. As
, this
condition is met when
.
Given a consumer's type w, valuations are i.i.d. for
all goods and uniformly distributed in
, i.e.,
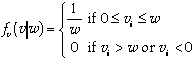
.
The probability that a consumer of type w will value any particular good at x
is for
. Thus the sum of valuations for
consumers with valuation at level x equals
, and
consequently the unbundled demand at price p is
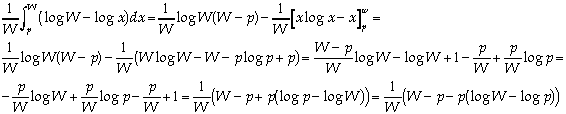
and thus .
As n increases, the mean valuation for a bundle of n goods by a consumer
of type converges stochastically to
.
Thus at a price per good for the bundle
, the seller will sell to
a fraction
of the consumers; i.e., those with type
. The resulting demand curve is
, and thus the
profit-maximizing bundle price is
per good, and the corresponding
average profits are
and the deadweight loss is
. If third-degree price discrimination is feasible, however, the seller
will set
, resulting in profits of
, no
deadweight loss, and full extraction of consumer surplus.
If a consumer of type with preferred consumption level
for the discriminating feature chooses a lower consumption level
, which is the preferred level for type
, the
resulting utility loss is
. That consumer values the bundle at
, and it can be shown that the optimal price schedule is linear: if a
consumer's consumption level for the discriminating feature implies type w, the
seller charges that consumer price
, which results in a
truth-telling equilibrium in which each consumer selects the level d implied by his
or her type w.
The resulting demand function is , with sales
at price
. The seller realizes profit
, where w* characterizes the marginal consumer that will
purchase the bundle. This profit can be calculated to be
, and
solving
yields
. Substituting dW
for w in the price schedule above yields the result in the Proposition.
Thus, unless , the optimal pricing strategy for the bundle
involves taking advantage of the feature d to price-discriminate. If
, then the seller is able to achieve third-degree price discrimination,
charging each consumer their reservation value for the bundle, and extracting the entire
consumer surplus, resulting in higher profits and no deadweight loss.
The proposed mechanism works as follows:
1. For each good i, expose a random subsample of si potential consumers to prices that make them reveal their demand for this good. These consumers will not have access to good i, which is normally in the bundle, unless they pay an additional price, pi.
2. Extrapolate the information from the subsamples to the rest of the population. If these si consumers are sufficiently representative, then their choices will provide a (noisy) signal of what the demand of the whole population, S, would have been for good i.
This mechanism requires preventing arbitrage among consumers, a
condition that can be enforced through technical means, such as public key encryption and
authentication; legal means, such as copyrights and patents; social sanctions, such as
norms against piracy; or combinations of the three. This mechanism will lead to a
deadweight loss for those si consumers
who are included in the sample, since some of them may choose to forgo consumption of the
good. If si = S, then the
mechanism provides exactly the same information as the conventional price system at
exactly the same cost. However, it is likely that for most purposes a sufficiently
accurate estimate of demand can be calculated for si << S, because of the rapidly declining informativeness (O()) of additional draws from the sample, as shown in Figure 6.
While the conventional price system provides only a binary signal of whether a given consumer's valuation is greater than or less than the market price, by offering different prices to different consumers one could estimate the shape of the entire demand curve, rather than just the portion near the market price. It may be too costly to experiment with prices far from the equilibrium price if all consumers must be offered the same price (Gal-Or, 1987), but if only a few consumers face off-equilibrium prices, then the costs can be kept manageable. Moreover, the shape of demand far from the equilibrium price is an important determinant of the total social surplus created by a good, and therefore the optimal investment policy regarding which types of goods should be created. For these reasons, our mechanism is likely to provide information about consumers' demand at a significantly lower social cost than the conventional price system, and it will never do worse.
Figure 6: Declining marginal benefits of larger samples
This statistical mechanism resembles the way investment decisions about certain information goods are actually made. For instance, information about consumers' valuations of individual television programs is rarely obtained by forcing them to pay for particular programs. Instead, television content producers provide a bundle of the goods for free (broadcast TV) or for a fixed price (cable or direct satellite TV) and rely on statistical sampling by firms like Nielsen and Arbitron to estimate audience size and quality. Advertising rates are based on these estimates, and indirectly determine which types of new television content will be produced. As discussed in section 6.4, this mechanism also resembles how royalties are apportioned to composers and songwriters from the revenues paid by nightclubs, restaurants, and other venues.
Finally, test-marketing of new products using focus groups also has
similarities with the mechanism we describe. In fact, any signal that is reliably
correlated with consumers' expected valuation for a good can serve as a substitute for the
information provided by the conventional price system. These indicators could include
prices from related product markets or populations, time spent visiting a site on the
World Wide Web, the number of keystrokes made while in a particular application, survey
answers on what users say they like, the expert opinion of product specialists, or ratings
generated by collaborative filtering mechanisms (see, e.g., Avery, Resnick &
Zeckhauser, 1995; Urban, Weinberg & Hauser, 1996).