Acknowledgments: The
authors
would like to thank Eric Clemons, Oliver Hart , Thomas Malone,
Haim Mendelson, two anonymous referees and the participants at
the MIT Center for Coordination Science Workshop on Supplier Relations,
the 4th Workshop on Information Systems and Economics, and IT
seminars at MIT, Boston University, New York University, and the
University of Rochester for their valuable comments. The National
Science Foundation and the Center for Coordination Science at
MIT provided generous support for this research.
This article uses the theory of incomplete contracts to illustrate that incentive considerations can motivate a buyer to limit the number of employed suppliers. To induce suppliers to make investments that cannot be specified and enforced in a satisfactory manner via a contractual mechanism, the buyer must commit not to expropriate the ex post surplus from such investments. Under reasonable bargaining mechanisms, such a commitment will be more credible if the buyer can choose from fewer alternative suppliers. Information technology increases the importance of noncontractible investments by suppliers, such as quality, responsiveness, and innovation; it is shown that when such investments are particularly important, firms will employ fewer suppliers, and this will be true even when search and transaction costs are very low.
As firms try to increase their performance, the interface with suppliers has become a major point of emphasis in the quest for additional efficiencies. This topic is enjoying increasing popularity, especially in view of the differences in customer-supplier relationships between Japanese and American firms. For instance, superior supplier relations have been estimated to provide a $300-600 per car cost advantage to Japanese manufacturers (Cole and Yakushiji 1984). These trends are reflected in the information technology (IT) literature as well, which has identified the impact of IT on supplier relationships as an important area for research, and has discussed these relationships in an institutional economics framework (Gurbaxani and Whang 1991, Malone et al. 1987), addressing the implications of firm size (Brynjolfsson et al. 1991) and the governance structure of the relationship (Clemons et al. 1993).
1.1. Transactional Considerations Predict More Suppliers
Determining the optimal number of suppliers is a natural extension of the "make versus buy" or "markets versus hierarchies" decision. Both questions can be analyzed by focusing on coordination costs. Malone, Yates and Benjamin (Malone et al. 1987) summarize this argument:
In a pure market, with many buyers and sellers, the buyer can compare many different possible suppliers of the product and select the one that provides the best combination of characteristics (such as design and price), thus presumably minimizing production costs for the desired product.... The coordination costs associated with this wide latitude of choice, however are relatively high, because the buyer must gather and analyze information from a variety of possible suppliers....
Hierarchies, on the other hand, restrict the procurer's choice of suppliers to the one supplier hierarchically connected to the procurer, either within a single company or in a closely linked relationship between two companies, [which] reduces coordination costs over those incurred in a market by eliminating the procurer's need to gather and analyze a great deal of information about various suppliers.
Malone, Yates & Benjamin argue further that IT will facilitate a move from single-supplier arrangements within the firm ("hierarchies") to multiple supplier arrangements ("markets") because it reduces the costs of coordination with suppliers:
Since the essence of coordination involves communication and processing information, the use of information technology seems likely to decrease these costs (e.g., see (Malone 1985)).
Similarly, in studying the impact of technology on the number of suppliers, IT researchers have focused on transactional considerations, examining trade-offs such as those between the increased search costs necessary to locate a large number of suppliers versus the increased probability of finding a better price or locating a superior product offering as a larger number of suppliers is surveyed. According to this logic, technological developments lowering the cost of acquiring information about prices and product characteristics in a given market should lead to an increase in the number of suppliers considered, especially in markets with differentiated products (Bakos 1991). Since it has been widely argued that information technology in general, and interorganizational systems, in particular, tend to lower search costs (Bakos 1987, Clemons and Row 1989, Malone 1985), as these systems are increasingly adopted in several sectors of the economy, they should lead to an increase in the number of suppliers employed by most firms.
1.2. Evidence of a Move to Fewer Suppliers
While there is evidence of a shift from single-supplier "hierarchies" to multiple supplier "markets" (Brynjolfsson et al. 1991, Johnston and Lawrence 1988), we have not observed a wholesale increase in the number of suppliers. On the contrary, there is significant recent evidence for an overall reduction in the number of suppliers, both as a general trend in certain industries, and as a by-product of information technology adoption in particular. For instance, a study of the automobile industry by Helper (1991a) found that the average number of suppliers decreased 25% between 1983 and 1988. In a survey of Japanese and American firms, Cusumano and Takeishi (1991) found that American firms were increasingly adopting the Japanese model of supplier relations, which involved relationships with about half as many suppliers per part (1.3 versus 2.8) and resulted in orders of magnitude fewer defects (0 to 0.01% in Japan versus 0.35 to 2.6% for American suppliers). In some industries the trend has been even more pronounced. Motorola reduced its supplier base from 10,000 to 3,000 in the past few years, prompting one industrial consulting firm to conclude that, "a revolution is going on in the relationships between suppliers and customers" (Emshwiller 1991).
The shift to fewer suppliers is often associated with the emergence of "strategic networks," such as those in the textile industry of central Italy (Antonelli 1988, Piore and Sabel 1984). Although there is a lack of formal empirical studies, anecdotal evidence abounds (Imai et al. 1985, Von Hipple 1986), and a recent review (Jarillo 1988) concluded that networking, especially in the Japanese Keiretsu model, was a theme in "practically all studies of industrial suppliers and industrial markets." In a similar vein, Johnston and Lawrence (1988) review several case studies and argue that "value-adding partnerships" (VAPs) in which each company "cultivates relationships with only a few (from two to six) suppliers for critical items" are supplanting not only vertically integrated hierarchies, but also arm's-length markets of multiple buyers and suppliers in the economy as a whole.
IT has been linked to these changes in several studies. Johnston and Lawrence specifically attribute the rise of VAPs in part to IT, including minicomputers and PCs, improved software, data standards, networking, and CAD/CAM. Helper found a statistically significant correlation between technology use and close supplier relations. Clemons, Reddi and Row (1993) also argue not only that there has been a recent "move to the middle" from both ends of the markets-hierarchies spectrum, but also that IT has been a significant driving force behind this trend.
This move to fewer suppliers in the face of declining coordination costs, including search costs and transaction costs, presents a paradox since it is at odds with the arguments discussed in section 1.1.
1.3. Explanations for the Move to Fewer Suppliers
One possible explanation for the shift to fewer suppliers is that search and coordination costs have actually increased. For example, if there are fixed technological and organizational investments required to connect to a supplier, a firm may wish to limit the number of suppliers it does business with to economize on these fixed costs. Similarly, if investments in electronic integration are specific to a particular supplier and thus are not transferable to new relationships, they may create switching costs limiting the desirable number of suppliers over a period of time. For example, investing in an interorganizational system for the exchange of component blueprints in a CAD format used by a certain supplier may limit the ability of the firm to explore new potential suppliers.
Although arguments such as these may explain why investment in interorganizational information systems could reduce the number of suppliers initially, it is widely believed that information technology lowers fixed costs and switching costs in the long run, principally because information technology standards can decrease the specificity of investment in interorganizational relationships (Clemons et al. 1993). For example, once an Electronic Data Interchange standard has been adopted in an industry, the cost of basic electronic integration between any supplier and buyer who have implemented this standard will be relatively small. In the long run, the optimal number of suppliers is determined by the marginal cost of adding additional suppliers, not the initial cost of establishing or joining a system. Thus any decrease in the number of suppliers resulting from an effort to reduce the adoption cost of information technology is likely to be temporary. The increase in outsourcing throughout the economy suggests that, on balance, there has not been an increase in transaction costs. Furthermore, direct measures of most basic types of computer-aided transactions show rapid cost declines, ranging as high as 25% per year (Brynjolfsson et al. 1991). Overall, the theoretical and empirical evidence appears to weigh heavily on the side of reduced coordination costs in the past decade.
A second possible explanation is that economies of scale have increased so much that it is only worthwhile to deal with a few large suppliers. Although this may be true in a few industries, the weight of the evidence does not support this hypothesis in general. Flexible manufacturing is widely acknowledged to have reduced the average size of production runs and overall set-up costs, enabling smaller plants and firms to compete successfully. For instance, in the automobile industry, lot sizes for both production and delivery were smaller in 1989 than five years earlier [1] (Helper 1991a). Furthermore, trends in information technology strongly favor smaller and cheaper computers and reduced economies of scale in production. Finally, the average size of firms has decreased in the past decade in the U.S. economy as a whole (Brynjolfsson et al. 1991).
A third possibility is that flexible manufacturing has enabled each supplier to offer a broader range of products. As a result, the buyer might be able to rely on fewer suppliers in total, but still have the same number for each product. [2] Although theoretically intriguing, this hypothesis could not explain the finding of Helper (1991a, 1991b) that the average number of competitors producing the same product for a given customer decreased from 2 to 1.5 and the number of rivals producing similar products in the auto industry fell from 2.3 in 1983 to 1.9 in 1988.
If this shift to fewer suppliers is not driven simply by changes in coordination costs, economies of scale, or supplier versatility, business leaders suggest an alternative explanation. According to Percy Barnevik, head of the $29-billion ABB conglomerate, price is less important than benefits such as responsiveness and higher quality:
"If you have ten suppliers for porcelain for your transformers ... you can cut those ten down to three." Because this approach gives each remaining supplier more business, ABB feels it can demand short delivery times and high quality.
"Any idiot can reduce a price by 10% to become more competitive. But if you can off an electric power transmission cable under the Baltic one year earlier than your competitor can, that is of tremendous value to the customer." (Rapoport 1992)
In fact, several field studies of buyer-supplier relations focus on the advantages that smaller and tighter networks of suppliers have, not only in quality (Cusumano and Takeishi 1991, Helper 1991b, McMillan 1990) and responsiveness (Johnston and Lawrence 1988), but also in innovation and technology adoption (Helper 1991a, Helper 1991b), defect rates (Cusumano and Takeishi 1991), trust (Johnston and Lawrence 1988) ,and information exchanges (Cusumano and Takeishi 1991, Helper 1991a, Helper 1991b). All of these characteristics involve investments by suppliers that are difficult or impossible to specify in advance in a contract, in other words they are "noncontractible," and they offer benefits that are largely specific to a particular buyer-supplier relationship. As discussed in the remainder of this paper, providing incentives for such investments presents special challenges. IT is likely to increase the importance of non-contractible factors, such as innovation, speed, responsiveness, and flexibility, emphasizing the need to address these challenges.
When investments are noncontractible and specific, firms must depend on their own ex post bargaining power (and/or the goodwill of their partners) to reap a share of the benefits created by their investments. [3] It has proven difficult to model these considerations in the past, for the same reasons that it is difficult to specify them in a contract, and as a result they have largely been ignored in the more formal literature on buyer-supplier relations. Notable exceptions include Clemons, Reddi and Row (1993), Helper (1991a), and Pisano and Chew (1990). Even these alternative approaches, however, do not explicitly address the question of how to provide incentives for supplier investment in quality, responsiveness, and innovation, and, specifically, how the number of suppliers affects the incentives to make such investments. In fact, the idea that limiting the number of suppliers, and thereby increasing their bargaining power, could be a successful competitive strategy, runs counter not only to standard neoclassical economic models, but to the widely used competitive strategy models as well (Porter 1980). As Alan Blinder put it: "Keiretsu are often portrayed as exclusionary devices that make Japanese companies unduly clannish and insular. How can such apparently restrictive business practices promote efficiency?" (Blinder 1991)
This article builds on the existing literature by adding incentive considerations to the coordination cost considerations in determining the optimal number of suppliers. In particular, we use the incomplete contracting framework developed by Grossman, Hart and Moore (Grossman and Hart 1986, Hart and Moore 1990) to show that when it is important to provide incentives for suppliers to make noncontractible investments, it can be optimal to limit the number of suppliers with which a buyer enters into a relationship. The intuition for this result is that a supplier will be able to garner more of the benefit created by his or her investment if the buyer does not have too many alternative suppliers. As a result, the supplier will have greater ex post bargaining power and, therefore, greater ex ante incentives to make noncontractible investments, such as investments in quality, responsiveness and innovation. Our analysis thus provides a partial formalization for the increasingly popular idea of partnership between buyers and suppliers (Henderson and Venkatraman 1990, Johnston and Lawrence 1988), which mirrors our emphasis on the incentive benefits of a tighter relationship with fewer suppliers.
Studying the role of incomplete contracting considerations in determining the optimal number of suppliers provides an alternative perspective and an additional explanation for the "move to the middle." In addition, whereas technological progress, such as the development of standards, tends to alleviate quickly technological barriers to increasing the number of suppliers, the incomplete contracting considerations are more resistant to technological solutions, and are thus likely to remain in place for the foreseeable future. We show that even if search and coordination costs were to go to zero, it can still be optimal for a firm to limit the number of suppliers it uses.
Section 2 presents a simple model that captures the basic idea of the trade-off between coordination costs and supplier fit. Considering only these factors leads to the conclusion that the number of suppliers should increase as coordination costs decline. Section 3 introduces the theory of incomplete contracts and models the incentive implications of increasing the number of suppliers, showing that the need to provide incentives for noncontractible supplier investments can limit the desirable number of suppliers. Section 4 presents an integrated model that includes the impact of coordination costs, fit, and incentives on determining the optimal number of suppliers. Section 5 concludes with implications of the model and some validating examples.
2. Coordination Costs and the Optimal Number of Suppliers
A natural approach to determining the optimal number of suppliers is to start from the assumption that a firm would benefit by increasing the number of its suppliers, thereby broadening its choice, but that technological considerations constrain this strategy. In this perspective, the number of suppliers is limited by considerations such as the cost of setting up a relationship, search costs, and transaction costs, which can generally be summarized as coordination costs.
For example, in trying to determine the optimal number of suppliers for a given input, it may be assumed that suppliers' product offerings are substitutes for one another, except that they differ in some desirable feature, such as price, fit, or product characteristics. Interacting with each supplier entails a coordination cost. After surveying some number of suppliers, the buyer selects the product offering that provides the best value according to its set of criteria. The optimal number of suppliers is determined by trading off the cost of further searches against the expected benefit from identifying a better supplier. To illustrate these trade-offs, in this section we offer a model for the optimal number of suppliers in the neoclassical tradition of Stigler (1951).
Consider a two-period setting with a buyer firm and
N risk-neutral potential suppliers with identical production
technology facing the same marginal cost, assumed to be zero.
Supplier offerings differ in a product characteristic, which,
without loss of generality, is assumed to be one-dimensional,
providing to the buyer firm utility e distributed in the interval
[0,1] according to a known density function fe;
e can be thought of as a "fit" indicator. Suppliers'
e can be discovered only after a relationship has been
established between the buyer firm and the corresponding supplier.
The buyer firm faces an irreversible cost K for each supplier
it does business with, which can be thought of as a coordination
cost. In the first period, the buyer firm selects n suppliers
from the N available suppliers (n ![]() N)
as the suppliers it will do business with. In the second period,
the buyer discovers the values of the fit parameters ei
for the suppliers, and purchases from the supplier whose offering
provides the "best match" (i.e., the highest e). [4]
N)
as the suppliers it will do business with. In the second period,
the buyer discovers the values of the fit parameters ei
for the suppliers, and purchases from the supplier whose offering
provides the "best match" (i.e., the highest e). [4]
To simplify the analysis, assume that competition between the suppliers drives prices to their marginal cost, thus allowing the buyer firm to appropriate the entire surplus. [5] The buyer selects the number of suppliers n, to maximize its expected surplus:
The resulting optimal number of suppliers n* is the largest integer satisfying the difference equation:
It is easy to see that the expected surplus
is maximized for a finite n*, as
is strictly decreasing and approaches zero as n approaches infinity, while k is constant.
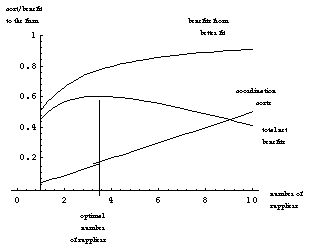
Figure 1 illustrates the tradeoff between coordination cost and fit as a profit maximization problem, under the assumption that the ei are independently distributed uniformly in the interval [0,1], so that
and coordination costs are k=0.05.
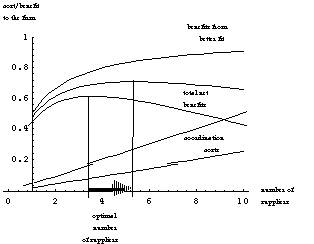
As mentioned earlier, it is widely believed that information technology lowers the costs of interfirm coordination (e.g., see (Malone et al. 1987)). Thus, according to these arguments, information technology is likely to favor an increase in the number of suppliers. Figure 2 illustrates this effect in the context of our simplified model by reducing coordination costs from k = 0.05 to k = 0.025. Formally, we have
![]() (1)
(1)
which becomes
where ![]() is the arbitrary cumulative
distribution for each of the ei. Since
is the arbitrary cumulative
distribution for each of the ei. Since ![]() ,
we know that the left-hand side of Equation (1) is decreasing
in n. Therefore, lower search costs, k, will be
associated with a larger number of suppliers, n. Figure
3 shows a plot of contour curves for buyer surplus. The darker
shading of the lower contours indicates the increase in buyer
surplus, and it can be seen how the optimal number of suppliers
increases as search costs decline.
,
we know that the left-hand side of Equation (1) is decreasing
in n. Therefore, lower search costs, k, will be
associated with a larger number of suppliers, n. Figure
3 shows a plot of contour curves for buyer surplus. The darker
shading of the lower contours indicates the increase in buyer
surplus, and it can be seen how the optimal number of suppliers
increases as search costs decline.
| search cost | 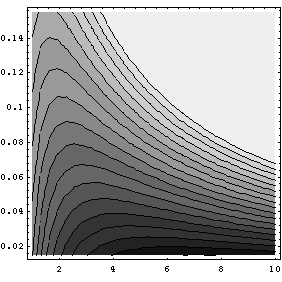 |
number of suppliers |
3. Incomplete Contracting and the Optimal Number of Suppliers
As shown in Model 1, ceteris paribus, optimizing buyers will never reduce the number of suppliers when coordination costs decrease. This leads us to consider other factors. In particular, we draw on the incomplete contracting literature to model the relationship between a firm and its suppliers focusing on incentive considerations, thereby capturing the incentive effects discussed in Section 1.3. As shown below, increasing the number of suppliers will reduce substantially the portion of the marginal returns on investment appropriated by each supplier. This will limit the suppliers' incentive to invest, and if supplier investment is critical, it can result in a suboptimal outcome. The remainder of this section formalizes this argument.
3.1. Incomplete Contracts Approach
Williamson (1975) has argued that complete contracts (in the sense that they never need to be renegotiated or revised) are costly or even infeasible. Grossman and Hart (1986) and Hart and Moore (1990) sharpen Williamson' s argument by pointing out that certain variables may not be verifiable by a third party, such as a court or an arbitrator, although they can be observed by the parties involved in the relationship. In judging a supplier's record for innovation, for example, both the firm and the supplier may be able to observe whether the supplier has been innovative and estimate the resulting value created, but it may not be possible to show that to the satisfaction of a court. Parties cannot enter into a contract based on the outcome of such variables, but instead must divide any resulting value through ex post bargaining. [6]
Thus the ex post bargaining power of each party will be taken into account before they make investments that create value but are not contractible. Changes in the structure of the relationship that affect each party's bargaining power will therefore have effects on equilibrium output. Based on this principle, we can analyze how changes in the number of suppliers affect their bargaining power and, therefore, their incentives to invest in the relationship and ultimately economic output.
3.2. An Incomplete Contracting Model for the Optimal Number of Suppliers
Now develop a model that considers how the number of suppliers affects the incentives of the buyer firm and its suppliers to invest in their relationship. To this end, we assume that the buyer firm and its suppliers must invest in some activity that affects the value realized, but is not feasible to describe in a comprehensive contract. This may be an investment in quality, responsiveness, or innovation, for example, an information system that promote "electronic integration" between the buyer and the suppliers, such as order entry, just-in-time inventory management, or electronic exchange of product designs. The supplier and the buyers must make investments specific to this relationship, such as identifying and suggesting improvements in product design. These investments will have little value in alternative uses, whereas their benefits are likely to be observable by the parties involved, but not verifiable by an outside arbitrator or a court of law.
Consider a two-period setting with N + 1 risk
neutral firms indexed by i = 0,1, . . ., N, including
a buyer firm (i = 0) and N identical suppliers (i
= 1, . . . , N) connected via an interorganizational system.
Before the first period, the buyer determines the number of suppliers
n participating in the system, which are the only suppliers
from which it can order goods. We assume that n cannot
be changed until after the second period. [7] All N
suppliers
possess identical technology, and, in the first period, each firm
i makes a private, nonverifiable investment xi at
cost c0(x0) for i = 0, andcs(xi),
for 1 ![]() i
i ![]() N,
to
which we refer as the
firm's noncontractible investment. In the second period, production
takes place, the goods are delivered, and payments are made. We
assume that once the investments are made, the marginal cost of
actually producing the product is zero. A set of firms
N,
to
which we refer as the
firm's noncontractible investment. In the second period, production
takes place, the goods are delivered, and payments are made. We
assume that once the investments are made, the marginal cost of
actually producing the product is zero. A set of firms ![]() can generate value v(S,x), where
can generate value v(S,x), where ![]() is the set of firms {0,1, . . ., N}, and x is the
vector of investments. The buyer (firm 0) requires access to at
least one of the suppliers to create any value, whereas each
supplier needs access to the buyer to create value. Suppliers
face no capacity constraints and only the total surplus is observable; [8]
thus, once investments have been made, there is no loss on expectation
from excluding any single supplier, if an alternative supplier
exists. In particular, in this case the value of a coalition is
given by
is the set of firms {0,1, . . ., N}, and x is the
vector of investments. The buyer (firm 0) requires access to at
least one of the suppliers to create any value, whereas each
supplier needs access to the buyer to create value. Suppliers
face no capacity constraints and only the total surplus is observable; [8]
thus, once investments have been made, there is no loss on expectation
from excluding any single supplier, if an alternative supplier
exists. In particular, in this case the value of a coalition is
given by
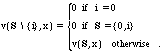
We also make the standard assumption of increasing marginal costs of investment and diminishing marginal returns to investment:
![]() ,
, ![]() ,
,
![]() and
and ![]() .
.
We assume that although noncontractible investments by the buyer firm and its suppliers are too complex to include in a contract, the total value produced is observable by all parties, so that bargaining in the second period takes place under symmetric information; in the terminology of Grossman and Hart, the total surplus generated is observable, but not verifiable (e.g., the buyer firm and its suppliers can observe quality, but they cannot write a contract contingent on the quality of the goods delivered). Since no contract can be written contingent on firm investments or the value generated by them, the total surplus generated in the second period will be apportioned according to the relative bargaining power of the parties involved.
There are a variety of bargaining models that could be applied to determine the outcome, for definiteness, we follow Hart and Moore (1990) in assuming that Nash bargaining takes place and that consequently each participant will receive a share of the payoffs proportionate to its Shapley value. In addition, we assume that all parties know this, and as a result this division of the surplus is mutually acceptable and is reached without any additional bargaining costs. In this setting, the firms' Shapley values are given by:
![]() , (2)
, (2)
where
![]()
s _ the number of agents in a given subset S
I _ the total number of agents
x = (x0, x1, ... ,xn) is the vector of individual investments.
Division of surplus according to the Shapley values amounts to paying each firm an amount equal to its contribution to the value of each potential coalition, multiplied by the probability that that particular coalition will be observed. [9]Under this formulation, firms that are not easily replaced will have more bargaining power and, thus, will be able to garner a larger share of the surplus generated from transacting. In our setting, each of the n identical suppliers will have some bargaining power and will receive some payments, therefore it is natural to consider each of them to be delivering a share of the goods supplied.
We now solve for equilibrium investment and output. The ex post bargaining power of the parties will have a considerable effect on the ex ante incentives to make noncontractible investments: Each firm will invest until the marginal benefit it can expect to receive equals the marginal cost of investment. For example, in a bilateral setting with a single buyer and a single supplier, each firm will invest until the marginal benefit it can expect to receive, as given by its Shapley value, equals the marginal cost of investment, resulting in the following first order conditions for the buyer and supplier firms, where:
Buyer firm: ![]() (3a)
(3a)
Supplier firm: ![]() (3b)
(3b)
Because neither firm can capture 100% of the additional revenue resulting from its noncontractible investments, each will have a suboptimal incentive to invest. In particular, each firm will invest up to the point at which the marginal cost of investment is equal to just one-half of the marginal value created, since this is the proportion it will be able to appropriate under Nash bargaining. This is the familiar "hold-up" problem described by Klein, Crawford and Alchian (1978).
In general, the first-order conditions of buyer and supplier firms are given by
Buyer firm: ![]() (4a)
(4a)
Each supplier: ![]() (4b)
(4b)
where 1 ![]() i
i ![]() n. The optimal
number of suppliers is determined by choosing n = n*
so that the resulting investments x* maximize the social
surplus:
n. The optimal
number of suppliers is determined by choosing n = n*
so that the resulting investments x* maximize the social
surplus:
It is apparent from Equations (4a) and (4b) that as the number of suppliers, n, increases, underinvestment becomes less severe for the buyer but becomes even worse for the suppliers. For instance, with two suppliers, the buyer will invest to the point at which the marginal cost of its investment is equal to two-thirds of the marginal value created, whereas each supplier will invest to the point at which its marginal cost of investment is equal to one-sixth of the value created. Figure 4(a) shows this decline in investment incentives for the suppliers, and Figure 4(b) shows the corresponding increase in buyer incentives, as the number of suppliers increases.
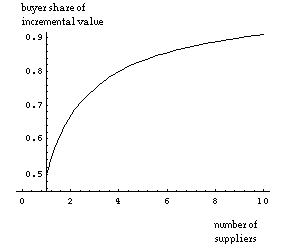
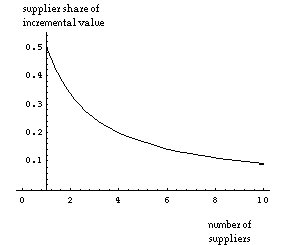
Figure 4a. Buyer incentives to invest. Figure 4b. Supplier incentives to invest.
If the buyer's noncontractible investment is very important relative to the suppliers' noncontractible investments, then this trade-off may be worth making. For example, if supplier investments in quality, responsiveness, and innovation have no impact on the total value created, the buyer should adopt the maximum feasible number of suppliers, in which case the buyer keeps almost all surplus, but no supplier will make any significant noncontractible investment. Conversely, if the buyer wishes to induce its suppliers to make significant noncontractible investments, then it must commit to buying only from a relatively small number of possible suppliers. Although the buyer will be able to keep a smaller fraction of the surplus generated, reducing the number of suppliers will induce each of them to make noncontractible investments, and thus will increase the total surplus to be divided. In other words, as the noncontractible supplier investments become more important, the optimal number of suppliers decreases. Conversely, as the noncontractible buyer investments become more important, the optimal number of suppliers increases.
To illustrate the analysis of this section, we can show how production incentives are affected by the number of suppliers, assuming a production function
with declining marginal returns of investment (0
![]() a, b
a, b ![]() 1). The
parameter
A characterizes
the relative importance of noncontractible buyer investment: For
example, as A decreases, it may signify that buyer investment
in innovation becomes relatively less important than supplier
investment in innovation. Assuming quadratic investment costs
1). The
parameter
A characterizes
the relative importance of noncontractible buyer investment: For
example, as A decreases, it may signify that buyer investment
in innovation becomes relatively less important than supplier
investment in innovation. Assuming quadratic investment costs
![]() , the marginal return on buyer investment
is
, the marginal return on buyer investment
is ![]() , and the marginal cost is
, and the marginal cost is ![]() .
Thus the equilibrium buyer investment
.
Thus the equilibrium buyer investment ![]() satisfies the first order condition
satisfies the first order condition
![]() . (5a)
. (5a)
Similarly, the marginal return on supplier i's investment
is ![]() and the marginal cost is
and the marginal cost is ![]() ,
giving us the corresponding first-order condition for the equilibrium
supplier investment
,
giving us the corresponding first-order condition for the equilibrium
supplier investment ![]() :
:
![]() (5b)
(5b)
Solving Equations (5) we get
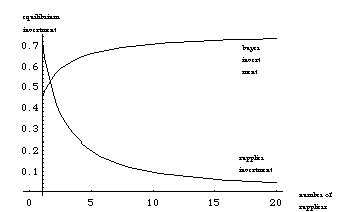
Figure 5 shows that buyer investment increases and supplier investment decreases as the number of suppliers increases.
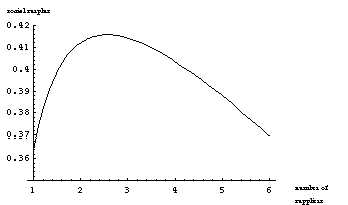
The resulting net social surplus is
Figure 6 plots the social surplus generated by the buyer and supplier investments in Figure 5, and shows how decreasing the number of suppliers can lead to a more efficient equilibrium, increasing the total social surplus created.[11]
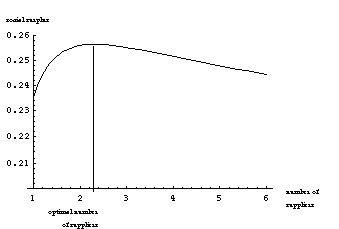
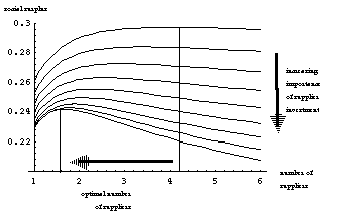
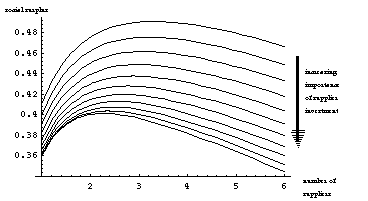
Figure 7 shows how an increase in the importance of supplier incentives (achieved parametrically by decreasing A) can lead to a reduction in the optimal number of suppliers.
4. Combining Incentive Considerations with Neoclassical Considerations
In this section we develop an integrated model that combines incentive considerations with neoclassical considerations to derive the optimum number of suppliers. The setting is similar to Model 2, except that, like Model 1, we incorporate a fixed coordination cost associated with each potential supplier, and we assume that supplier product offerings are heterogeneous in some contractible characteristic, thus providing the buyer firm with the incentive to search the supplier market for the product with the best "fit."
Consider a two-period setting with N + 1 risk neutral firms indexed by i = 0,1, . . . N, including a buyer firm (i = 0) and N identical suppliers (i = 1, . . . , N). The buyer firm faces an irreversible setup cost k for each supplier it does business with, which can be thought of as a coordination cost. Before the first period, the buyer selects n suppliers to do business with. The supplier offerings consist of two parts: a contractible feature ("fit") and a noncontractible feature (e.g., quality, responsiveness, or innovation).
In the first period, each firm i makes a private,
nonverifiable investment xi at cost c0(x0)
for i = 0, andcs(xi), for 1 ![]() i
i
![]() N, to which we refer as noncontractible investments. All
suppliers possess identical technology ex ante and there
are no binding capacity constraints, so that the buyer can make
a credible threat to shift the order to any other supplier. As
in Model 2, the total noncontractible value created is a function
of all parties' invesments: v =v(
N, to which we refer as noncontractible investments. All
suppliers possess identical technology ex ante and there
are no binding capacity constraints, so that the buyer can make
a credible threat to shift the order to any other supplier. As
in Model 2, the total noncontractible value created is a function
of all parties' invesments: v =v(![]() ,x).
Once again, we assume increasing marginal costs and diminishing
marginal returns to investment, that is
,x).
Once again, we assume increasing marginal costs and diminishing
marginal returns to investment, that is
![]() ,
, ![]() ,
,
![]() and
and ![]() ,
,
which guarantee the existence and uniqueness of and equilibrium with symmetric supplier investments.
In addition to their noncontractible attributes, such as innovation, supplier offerings also differ in "fit." Without loss of generality, fit is assumed to be one-dimensional and to provide the buyer utility e, distributed in the interval [0, emax] according to a known density function fe. Supplier e's can be discovered only after a relationship has been established between the buyer firm and the particular supplier, and are ex post observable by the buyer firm and all n suppliers.
In the second period, the noncontractible value,
v(![]() ,x), is realized, the buyer
licenses the contractible feature from the most desirable supplier
(max e) thereby generating total value m(
,x), is realized, the buyer
licenses the contractible feature from the most desirable supplier
(max e) thereby generating total value m(![]() ,x)
= v(
,x)
= v(![]() ,x) + maxe,
production
takes place, the goods are delivered, and payments are made. As
in Model 2, each of the n suppliers provides some portion
of total output and gets a share of the surplus based on its bargaining
power. Investments are specific to this setting, and the buyer
must gain access to at least one supplier (e.g., by purchasing
from that supplier) to create value. Similar to Model 2, the value
of a coalition S is given by
,x) + maxe,
production
takes place, the goods are delivered, and payments are made. As
in Model 2, each of the n suppliers provides some portion
of total output and gets a share of the surplus based on its bargaining
power. Investments are specific to this setting, and the buyer
must gain access to at least one supplier (e.g., by purchasing
from that supplier) to create value. Similar to Model 2, the value
of a coalition S is given by
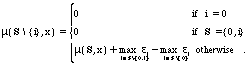
Excluding supplier i from a coalition would reduce total value if, and only if, ei is larger than the e's of all other suppliers in the coalition, when the ability to licence ei is lost to the rest of the coalition. Supplier i will not reduce the noncontractible portion of a coalition's value as long as there is at least one other supplier in the coalition. Conversely, if the buyer were to leave a coalition, it would incrementally reduce the value created by the coalition by its entire amount, to zero.
Since no contract can be written contingent on firm investments or the value generated by them, the total surplus generated in the second period will be apportioned according the relative bargaining power of the parties involved; as before, we assume that this bargaining satisfies the Nash requirements, is costless, and leads to a division of the surplus according to Shapley values.
The Shapley values are given by Equation (1), adding the random fit variable e:
![]() (6)
(6)
where
![]()
![]()
![]()
![]()
s _ number of agents in a given subset S
I _ total number of agents
x = (x0, x1, . . . ,xn) is the vector of individual investments
We now examine what happens to the noncontractible
investments as the number of suppliers changes. Whereas the suppliers
are ex ante identical, this symmetry is violated in the
second-period bargaining because of the differences in their products.
The result is that if there are multiple suppliers, although all
noncontractible supplier investments xi (i ![]() 1) are symmetric, suppliers with favorable product characteristics
(large e) are able to appropriate proportionally more value
than the ones with undesirable product characteristics (small
e), since by leaving a coalition they create a bigger reduction
in value.
1) are symmetric, suppliers with favorable product characteristics
(large e) are able to appropriate proportionally more value
than the ones with undesirable product characteristics (small
e), since by leaving a coalition they create a bigger reduction
in value.
The share of output that each party can expect to receive will determine their incentives to invest. This is reflected in the first-order conditions. For the buyer firm, equilibrium investment satisfies [12]
Buyer firm: ![]() (7a)
(7a)
where ![]() is the distribution
function for the kth-order statistic for random variable
e. Because of symmetry, the first-order conditions for
the suppliers are
is the distribution
function for the kth-order statistic for random variable
e. Because of symmetry, the first-order conditions for
the suppliers are
Each supplier: ![]() (7b)
(7b)
The optimal number of suppliers n will maximize total surplus, taking into account the connection and coordination costs k(n) and the benefits from improved fit as the number of suppliers increases, as well as the impact on buyer incentives and seller incentives. More formally, n will maximize
where x* is given by the first-order conditions of Equations (7).
As in Model 2, if the buyer wishes to induce significant noncontractible investment from its suppliers, it must commit to buying only from a relatively small number of possible suppliers. From Equations (7), ceteris paribus, if the suppliers' noncontractible actions become more important, then the optimal number of suppliers decreases. Conversely, if the buyers' noncontractible actions become more important, the optimal number of suppliers increases. The basic effects of fit (improving as n increases) and coordination costs (increasing with n), which were analyzed in Model 1, also apply in Model 3. The final equilibrium value of n will balance all of these forces and will lie between the equilibrium of Model 1 (which ignored incentives) and that of Model 2 (which ignored coordination costs and fit).
We illustrate the analysis of this section by extending the parametric example developed in Section 3.3. We use the same production function
and quadratic investment costs ![]() ,
adding a uniformly distributed fit parameter and a constant coordination
cost per supplier. The results of Section 3.3 qualitatively persist,
except that when coordination costs are high, large numbers of
suppliers become less attractive. Figures 8 and 9 correspond
to Figures 6 and 7 in Section 3.3. [13]
,
adding a uniformly distributed fit parameter and a constant coordination
cost per supplier. The results of Section 3.3 qualitatively persist,
except that when coordination costs are high, large numbers of
suppliers become less attractive. Figures 8 and 9 correspond
to Figures 6 and 7 in Section 3.3. [13]
The last decade has witnessed significant changes in both the technology and the organization of buyer-supplier relations, providing an opportunity to re-examine our theories. The persistence and even proliferation of small networks of suppliers as search and transaction costs have declined suggests that previous theories were incomplete. Drawing on evidence that the principal benefits of reducing the number of suppliers lie in the resulting incentives make noncontractible investments such as quality, responsiveness, and innovation, rather than any reduction in coordination costs, we were able to develop a more comprehensive model.
5.1. Implications of the Model
Our model leads to some interesting predictions. First, when noncontractible supplier investments are important, we find that it may be optimal to work with only a small number of suppliers even if search and transaction costs become negligible. In other words, although technological advances that reduce coordination costs will generally increase efficiency, when they also increase the importance of noncontractible supplier investments, such as investments in quality, responsiveness, and innovation, they do not necessarily lead to an increase in the number of suppliers used by a firm. Thus our model addresses the basic paradox posed in Section 1.2.
Second, our model predicts that the number of suppliers will be related inversely to the importance of providing suppliers with incentives to make noncontractible investments. This can explain the finding of Cusumano and Takeishi of a strong correlation between the number of suppliers and the importance of certain dimensions of the relationship (see Table 1).
| Dimension | U.S. firms | Japanese firms | |
| 1. Number of suppliers | Many | Fewer | |
| 2. Selection criteria | Price | Quality, price, etc. | |
| 3. Role in development | Smaller | Larger | |
| 4. Pricing practices | Competitive bids | Target Prices | |
| 5. Price changes | Upward | Downward | |
| 6. Defect rates | Higher | Lower | |
| 7. Quality improvement | Lower | Higher | |
| 8. Information exchanges | Lower | Higher | |
| 9. Suggestions to Suppliers | Few | Many |
In our interpretation, each of the dimensions 2 through 8 in Table 1 is indicative of an important, noncontractible investment on the part of the supplier, and a correspondingly smaller reliance on explicit contracts to govern the relationship. According to our model, the role of noncontractible factors such as quality, responsiveness, and innovation in supplier selection, and the suppliers' continuing effort to improve these characteristics even after they are selected, go hand-in-hand with the reliance on fewer suppliers.
This sort of empirical correlation is not unique to Cusumano and Takeishi. The advantages of close buyer-supplier relations, such as quality, trust, innovation, information sharing and responsiveness that are highlighted by other authors (Antonelli 1988, Helper 1991a, Helper 1991b, Johnston and Lawrence 1988, McMillan 1990) are also exactly those dimensions most difficult to contract for explicitly. In particular, our model provides a way of formalizing and explaining the contrasting observations that "General Motors Corp.'s suppliers enjoy less security [than the Japanese] and hence have less reason to invest in the relationship" (Blinder 1991) and that "[S]ince an implicit/explicit arrangement of profit sharing is the normal practice in [the Japanese supplier] relationship, under investment in transaction-specific assets may be avoided to both parties' mutual advantage." (Aoki 1986)
The effectiveness of the strategy of reducing the number of suppliers to improve incentives for quality is supported by the experiences of companies such as Xerox, which has reduced its supplier base from 5000 to about 500, and has seen its reject rates on parts go down by a factor of 13 (Emshwiller 1991).
It is worth noting, however, that our model predicts that reducing the number of suppliers will not always be beneficial. If the importance of specific, noncontractible investments by suppliers is relatively low, then it is optimal to increase the number of suppliers searched until the marginal cost of search equals the expected marginal benefit from improved fit. For example, incentive considerations effectively can be ignored for easily specified products such as commodities. For these products, continued reductions in coordination costs should lead to an increase in the number of suppliers considered.
There is a second situation under which reducing the number of suppliers may be unwise. According to our model, reducing the number of suppliers will reduce the incentives of the buyer to make noncontractible investments, because the buyer's bargaining power is weakened. Thus, when it is relatively more important for the buyer to make such investments, we should expect the buyer to keep his or her options open with a larger number of suppliers. The decisions by IBM and other computer manufacturers to second- and third- source some of their vital components, such as ICs, is consistent with a desire to prevent any one supplier from having too much bargaining power. In this way, they can hang on to more of the surplus resulting from their investments in innovation and other noncontractibles.
Finally, it should be noted that the number of suppliers that strikes the optimal balance between buyer and supplier incentives (as analyzed in Model 2), in general, will not happen to be the same as the number that strikes the optimal balance between coordination costs and fit (as analyzed in model 1). The number that balances all four forces (as analyzed in Model 3) will be a weighted average of the previous two optima, and its value will depend on the relative importance of incentives versus coordination costs. Thus if the importance of buyer and supplier incentives increases, the optimal number of suppliers employed will likely be reduced, even if the importance of both buyer and supplier incentives increases proportionately. For example, suppose the number of suppliers that provides the best net incentives for both the buyer and the suppliers to make noncontractible investments is 2, and, because of low coordination costs, the optimum balance between fit and coordination costs is reached with 100 suppliers. The overall optimum will then require between 2 and 100 suppliers. If it becomes more important to provide incentives for noncontractible investments such as information sharing or innovation, then the overall optimum will decrease so that it is closer to 2. This will happen even if the need for buyer incentives to make a noncontractible investment increases just as much as the need for supplier incentives to make such investments.
5.2. Role of IT in Reducing the Number of Suppliers
We have seen that the general trend toward fewer suppliers can be explained by the increasing emphasis placed by American firms on noncontractible supplier attributes such as innovation, quality, responsiveness, trust, and information sharing, epitomized by the "total quality management" theme popular in management circles. Furthermore, many of the other characteristics listed in Table 1 are getting increasing attention as well. It is possible that this new emphasis on noncontractible attributes represents an exogenous trend, perhaps due to a belated realization that noncontractible investments ultimately affect profits, or perhaps due to an increasingly fierce competitive environment. In this case, this trend is likely to counteract any increase in the number of suppliers caused by declining coordination costs.
We believe that information technology also plays an important role in facilitating this "move to the middle." Our model indicates that the mechanism behind this move entails the combination of reduced coordination costs with an increased need to emphasize noncontractible investments such as quality, responsiveness, and innovation, to remain competitive. Although the impact of lowering coordination costs has been discussed elsewhere (Bakos 1987, Malone et al. 1987), there are a number of reasons why IT will also increase the importance of noncontractible investments. For instance, just-in-time inventory systems require a very low tolerance for defects (O'Neal 1989). Milgrom and Roberts (1990) provide a formal model of "modern manufacturing" in which they argue that an emphasis on "quality" is a necessary complement for the successful use of "technologically advanced equipment."
Furthermore, exploiting IT to respond rapidly to changing market conditions may preclude detailed contracts or work rules. For instance, Brynjolfsson (1990a, 1990b) has argued that information technology tends to automate the more routine tasks, that are typically those which are easiest to detail in a contract, leaving behind a residue of tasks that are neither automatible nor contractible. He also suggests that cheap information can be a complement for knowledge-intensive tasks, and shows how this can lead to a decentralization of authority and incentives. Both of these effects would increase the need to rely on institutional mechanisms, such as reducing the number of suppliers, to provide appropriate supplier incentives.
More generally, IT has contributed to the increased importance of noncontractibles, such as speed, flexibility, and responsiveness throughout the economic environment, in the process increasing the number of future scenarios that would have to be considered and provided for in any comprehensive contract between a buyer and a supplier. Furthermore, we believe that IT is likely to create a relative advantage for institutional over contractual governance mechanisms. In particular, IT facilitates the tracking of a large number of variables, enabling the efficient gathering of vast amounts of data, thus creating a large number of possible future contingencies. Managerial judgment and filtering technologies such as decision support systems ensure that only few such contingencies will need to be addressed ex post; a comprehensive contract, however, would require the advance consideration and planning for all these possible outcomes.
As a result, it has become relatively more cost-effective for both parties to share the benefits of their relationship relying on trust and ex post bargaining. In such an environment, a good partner is one who does not adhere merely to the "letter of the contract," but one who does whatever reasonably needs to be done. This requires an increased reliance on the institutional incentives available to deal with incomplete contracts, such as "partnering," leading to reduced numbers of suppliers and long-term relationships. In effect, IT has led to a situation where the technology of production has outrun our ability to write contracts that keep pace. [14]
In a related stream of thought, Huber (1990) has pointed out the distinction between knowledge- and product-intensive relationships and activities. Knowledge-intensive activities are not as easily contractible, because of the difficulty of writing complete contracts that define them precisely in a way that allows legal description of the contingencies. As the widespread adoption of information technology increases the share of knowledge-related activities in the relationship between a firm and its suppliers, our analysis predicts that the significance of incomplete contracting considerations will increase.
Recent empirical evidence has highlighted the need to extend the theory of buyer-supplier relationships to account for the importance of incentive considerations. Ultimately, while technological developments are likely to continue to reduce the magnitude of coordination costs, the need to provide incentives for noncontractible investments is likely to remain an important factor in limiting the optimal number of suppliers.
| Ordering | B | 1 | 2 | 3 |
| B123 | ||||
| B132 | ||||
| B213 | ||||
| B231 | ||||
| B312 | ||||
| B321 | ||||
| 1B23 | ||||
| 1B32 | ||||
| 12B3 |
| |||
| 123B |
| |||
| 13B2 |
| |||
| 132B |
| |||
| 2B13 |
|
| ||
| 2B31 |
|
| ||
| 21B3 |
| |||
| 213B |
| |||
| 23B1 |
|
| ||
| 231B |
| |||
| 3B12 |
|
| ||
| 3B21 |
|
|
| |
| 31B2 |
| |||
| 312B |
| |||
| 32B1 |
|
| ||
| 321B |
| |||
|
Share of total payoff: |
|
|
|
|
In Table A1, each of the 24 ways (orderings) possible in forming
the grand coalition is considered, and the payoffs are calculated
on the assumption that the each party gets its incremental contribution
to the coalition. Blanks denote zero payoffs. For example, in
the first ordering, B123, the payoff to buyer B is zero, since
B adds no value to the coalition {B}\{B}=![]() .
Formally, m({B}, x) - m({B}\{B},x)
= 0. The payoff to supplier 1 is its incremental contribution
e1, since the
coalition
{B,1} creates value e1.
The payoff to supplier 2 is zero since the value of coalition
{B,1,2} is no greater than the value of coalition {B,1}. Similarly,
the payoff to supplier 3 is zero since the value of coalition
{B,1,2,3} is no greater than the value of coalition {B,1,2}. The
payoffs in each of the other possible orderings are calculated
similarly. Each party's Shapley value is then computed by summing
the individual payoffs, with equal weight for each possible ordering,
and thus deriving the final set of payoffs. Since each supplier
is equally likely ex ante to realize any given value of
e, the risk-neutral suppliers make their investment decisions
based on the average of the three possible supplier payoffs. The
resulting first order conditions for arbitrary n are given
by Equations (7a) (for the buyer) and (7b) (for the n suppliers).
An inductive proof for the buyer's share in Equation (7a) is given
below, while the suppliers' shares in Equation (7b) follow from
the ex ante symmetry.
.
Formally, m({B}, x) - m({B}\{B},x)
= 0. The payoff to supplier 1 is its incremental contribution
e1, since the
coalition
{B,1} creates value e1.
The payoff to supplier 2 is zero since the value of coalition
{B,1,2} is no greater than the value of coalition {B,1}. Similarly,
the payoff to supplier 3 is zero since the value of coalition
{B,1,2,3} is no greater than the value of coalition {B,1,2}. The
payoffs in each of the other possible orderings are calculated
similarly. Each party's Shapley value is then computed by summing
the individual payoffs, with equal weight for each possible ordering,
and thus deriving the final set of payoffs. Since each supplier
is equally likely ex ante to realize any given value of
e, the risk-neutral suppliers make their investment decisions
based on the average of the three possible supplier payoffs. The
resulting first order conditions for arbitrary n are given
by Equations (7a) (for the buyer) and (7b) (for the n suppliers).
An inductive proof for the buyer's share in Equation (7a) is given
below, while the suppliers' shares in Equation (7b) follow from
the ex ante symmetry.
Proof. Assume, without loss of generality, that suppliers are ordered by ek, that is, e1 > e2 > . . . > en. If there is only one supplier, then the buyer retains its Shapley payoff of one-half of e1 as its share of the "fit" surplus, that is, the buyer's share is given by
when n = 1. Assume the formula is true for
all n ![]() j . If n = j + 1,
then
for each of the (j + 1)! orderings of the j+1 firms
0, 1, ... j, there are j+2 corresponding orderings
of the firms 0, 1, ... j + 1,
each derived by adding firm j + 1. Since en+1 is
the smallest ei, the buyer's payoffs in the new orderings
change only when the buyer received nothing (by being first) in
the original ordering. There are j! orderings of firms
0, 1, . .. j in which the buyer (firm 0) is first, and
for each of these there is one of the corresponding j+2
orderings of firms 0, 1, ... j + 1
in which supplier j + 1 comes before firm 0; in that case
the buyer receives ej+1 as its payoff. Thus the buyer receives
ej+1 in j! out of the (j + 2)! possible orderings
of firms 0, 1, ... j + 1 for a
ratio of 1/j(j+2). Hence the buyer's share is still
given by
j . If n = j + 1,
then
for each of the (j + 1)! orderings of the j+1 firms
0, 1, ... j, there are j+2 corresponding orderings
of the firms 0, 1, ... j + 1,
each derived by adding firm j + 1. Since en+1 is
the smallest ei, the buyer's payoffs in the new orderings
change only when the buyer received nothing (by being first) in
the original ordering. There are j! orderings of firms
0, 1, . .. j in which the buyer (firm 0) is first, and
for each of these there is one of the corresponding j+2
orderings of firms 0, 1, ... j + 1
in which supplier j + 1 comes before firm 0; in that case
the buyer receives ej+1 as its payoff. Thus the buyer receives
ej+1 in j! out of the (j + 2)! possible orderings
of firms 0, 1, ... j + 1 for a
ratio of 1/j(j+2). Hence the buyer's share is still
given by
when n=j+1, and by induction the formula
is true for all n.
C. Antonelli, ed.. (1988). New Information Technology and Industrial Change: The Italian Case. Dordrecht: Kluwer Academic Publishers.
M. Aoki, (1986). "Horizontal versus Vertical Information Structure of the Firm.," The American Economic Review, Vol. 76, No. 5, pp. 971-983.
J. Y. Bakos, (1987) "Interorganizational Information Systems: Strategic Opportunities for Competition and Cooperation." Ph.D. Dissertation, Sloan School of Management, Massachusetts Institute of Technology, Cambridge.
J. Y. Bakos, (1991). "A Strategic Analysis of Electronic Marketplaces." MIS Quarterly, Vol. 15, No. 3, pp. 295-310.
J. Y. Bakos, and E. Brynjolfsson, (1993). "Why Information Technology Hasn't Increased the Optimal Number of Suppliers." In Proceedings of the 26th Hawaii International Conference on System Sciences, . Kailua-Kona, Hawaii: IEEE Press.
A.S. Blinder, (1991, October 14). "A Japanese Buddy System that could Benefit U.S. Business." Business Week, p. 32.
E. Brynjolfsson, (1990a). "Information Technology and the 'New Managerial Work'." Working Paper, Massachusetts Institute of Technology, Cambridge, MA.
E. Brynjolfsson, (1990b) "Information Technology and the Re-organization of Work: Theory and Evidence". Ph.D. Dissertation, Sloan School of Management, Massachusetts Institute of Technology, Cambridge, MA.
E. Brynjolfsson, T. Malone, V. Gurbaxani, and A. Kambil, (1991). "Does Information Technology Lead to Smaller Firms?" Technical Report 123. Massachusetts Institutue of Technology, Center Coordination Science, Cambridge, MA.
E.K. Clemons, S.P. Reddi, and M. Row.(1993). "The Impact of Information Technology on the Organization of Economic Activity: The "Move to the Middle" Hypothesis." Journal of Management Information Systems, September 1993 (in press).
E.K. Clemons, and M. Row (1989). "Information Technology and Economic Reorganization." In Proceedings of the 10th International Conference on Information Systems, (pp. 341-352). Boston, MA:
R. Cole, and K. Yakushiji. (1984). "The U.S. and Japanese Automotive Industries in Transition". Joint U.S. - Japan Automotive Study Ann Arbor, Michigan.
M.A. Cusumano, and A. Takeishi. (1991). "Supplier Relations and Management: A Survey of Japanese, Japanese-Transplant, and U.S. Auto Plants." Strategic Management Journal, Vol. 12, pp. 563-588.
J.R. Emshwiller. (1991, August 8). "Suppliers Struggle to Improve Quality as Big Firms Slash Their Vendor Rolls." Wall Street Journal, p. B1.
S. Grossman, and O. Hart. (1986). "The Costs and Benefits of Ownership: A Theory of Vertical and Lateral Integration." Journal of Political Economy, Vol. 4, pp.691-???.
F. GuL. (1989). "Bargaining Foundations of Shapley Value." Econometrica, Vol. 57, No. 1, pp. 81-95.
V. Gurbaxani, and S. Whang. (1991). "The Impact of Information Systems on Organizations and Markets." Communications of the ACM, Vol. 34, No. 1, pp. 59-73.
O. Hart, and J. Moore,. (1990). "Property Rights and the Nature of the Firm." Journal of Political Economy, Vol. 98, No. December, pp. 1119-1158.
S. Helper. (1991a). "How Much Has Really Changed between U.S. Automakers and Their Suppliers?" Sloan Management Review, pp. 15-27, Summer.
S. Helper. (1991b). "Supplier Relations and Investment in Automation: Results of Survey Research in the U.S. Auto Industry". Working Paper, Dept. of Economics, Case Western Reserve University, Cleveland, OH, September.
J. Henderson and N. Venkatraman,. (1990). "Strategic Alignment: A Model for Organizational Transformation via Information Technology". CISR/Sloan Working Paper, Massachusetts Institute of Technology, Cambridge, MA. November.
G.P. Huber. (1990). "A theory of the effects of advanced information technologies on organizational design, intelligence and decision making." Academy of Management Review, Vol. 15, No. 1, pp. 47-71.
K. Imai, I. Nonaka, and H. Takeuchi.(1985). "Managing new product development: How Japanese companies learn and unlearn." In K. B. Clarke, R. H. Hayes and C. Lorenz (Eds.), The Uneasy Alliance Boston, MA: Harvard Business School Press.
J.K. Jarillo. (1988). "On Strategic Networks." Strategic Management Journal, Vol. 9, No. , pp. 31-41.
R. Johnston and P. Lawrence. (1988). "Beyond Vertical Integration--the Rise of the Value-Adding Partnership," Harvard Business Review, Vol. No. July-August, pp. 94-101.
B. Klein, R. Crawford, and A. Alchian.(1978). "Vertical Integration, Appropriable Rents and the Competitive Contracting Process." Journal of Law and Economics, Vol. 21, PP. 297-326, October.
T.W. Malone. (1985). "Organizational Structure and Information Technology: Elements of Formal Theory." Working Paper 130. Center for Information Systems Research, Sloan School of Management, Massachusetts Institute of Technology, Cambridge, MA. August.
T.W. Malone, J. Yates, and R.I. Benjamin. (1987). "Electronic Markets and Electronic Hierarchies: Effects of Information Technology on Market Structure and Corporate Strategies." Communications of the ACM, Vol. 30, No. 6, pp. 484-497.
J. McMillan. (1990). "Managing Suppliers: Incentive Systems in Japanese and U.S. Industry." California Management Review, Vol. 32, No. 4, pp. 38-55.
P. Milgrom and J. Roberts.(1990). "The Economics of Modern Manufacturing: Technology, Strategy, and Organization." American Economic Review, Vol. 80, No. 3.
C.R. O'Neal. (1989). "JIT Procurement and Relationship Marketing." Industrial Marketing Management, Vol. 18, No. , pp. 55-63.
M. Piore and C. Sabel (1984). The Second Industrial Divide. New York: Basic Books.
G.P. Pisano and W.B. Chew,. (1990). "Vertical Integration, Long Term Contracts, and the Costs of Quality." Working Paper Harvard Business School. September.
M.E. Porter. (1980). Competitive Strategy. New York, NY: The Free Press.
Rapoport (1992, June). A Tough Swede Invades the U.S. Fortune, p. 78.
G.J. Stigler. (1951). "The Division of Labor is Limited by the Extent of the Market." Journal of Political Economy, Vol. LIX, No. 3, pp. 185-195.
E. Von Hipple. (1986). "Lead Users: a Source of Novel Product Concepts." Management Science, Vol. 32, No. 7, pp. pp. 791-805.
O. Williamson. (1975). Markets and Hierarchies:
Analysis and Antitrust Implications. New York: Free Press.
[*] University of California, Irvine
[**] Massachusetts Institute of Technology
[1]For example, the percentage of suppliers that deliver in lots that last their customer over eight days fell from 44 to 16%.
[2]We thank an anonymous referee for pointing out this possibility.
[3]An alternative is for the buyer and the supplier firms to internalize bargaining by vertically integrating. For the purposes of this article we assume that vertical integration is not a feasible alternative. It should be noted, however, that even when vertical integration is a feasible option, incentives may be improved under separate ownership (Grossman and Hart 1986), and thus the buyer and supplier firms may choose to remain under separate ownership.
[4]In this model only one supplier (the one with the best fit) is selected to provide the product purchased. Thus when we refer to n suppliers, the remaining n - 1 firms are "suppliers" in the sense that all of them are equally likely, ex ante, to be selected. Alternatively, in a multiperiod setting, the buyer firm may purchase from different suppliers in each period (assuming the [[epsilon]]'s are temporally independent), and thus all n firms will eventually be used as suppliers, and over time, a variety of suppliers will be seen to deliver goods.
[5]Relaxing this assumption and assuming that prices are determined by ex post bargaining does not qualitatively change the results. See the model in Section 4, for example. In addition, for an alternative interpretation of Model 1, the product can be considered a commodity, and 1 - [[epsilon]] can be the seller price, with a distribution exogenous to the model. In this case the firm buying from the supplier with the highest [[epsilon]] is equivalent to buying from the supplier offering the lowest price.
[6]Furthermore, in the absence of complete contracting, standard mechanism design arguments, such as those that invoke the revelation principle, are infeasible and, as shown by Hart and Moore (1990), optimal investment levels generally cannot be sustained.
[7]The choice of a finite n will effectively commit the buyer not to expropriate the entire noncontractible surplus from its relationship with the suppliers.
[8]For example, investments in electronic integration by the firm and its suppliers increase the value generated by the firm and its supplier network, but increases in value cannot be traced to the individual investments responsible for them.
[9]Although the Shapley value is traditionally used to analyze cooperative bargaining, (Gul 1989) provides a detailed noncooperative bargaining justification for this assumption. It can be useful to think of the Shapley value as the result of generalized Nash bargaining. In any event, the exact rule for division of the surplus will generally have no qualitative effect on the results as long as each agent's share of output is positively correlated with his or her access to essential assets via coalitions with other parties.
[10]This is the value of n that maximizes net social surplus. An alternative approach would be to assume that the buyer chooses n to maximize its private surplus B0(x*)v(,x*) - c0(x0), as in (Bakos and Brynjolfsson 1993). If side payments are allowed, however, then the socially optimal number of n will also maximize the buyer's individual payoff, since the buyer firm will be compensated via ex ante side payments for choosing the socially optimal institutional arrangement.
[11]Figures 5-7 were derived with [[alpha]] = [[beta]] = 0.9 and A = 0.6 in Figures 5 and 6 and ranging from 0.475 to 0.715 in Figure 7.
[12] See the appendix for an illustrative example when n = 3, and a general proof.
[13]Figures 8 and 9 were derived with [[alpha]] = [[beta]] = 0.9, A = 0.6 in Figure 8 and ranging from 0.475 to 0.775 in Figure 9, [[epsilon]]max = 0.3 and [[kappa]] = 0.02.
[14] Indeed, if the growing number of lawyers employed is any indication, we are far from automating the writing and enforcement of comprehensive contracts. Despite all the effort, gaps still remain in most contracts.