Abstract: This research proposes database decentralization
and incentive principles which drive information sharing and ultimately
system performance. Existing research has identified the benefits
of centralized control while formalizing the importance of setting
standards, enhancing user transparency, and reducing organization-wide
data inconsistency. In practice, however, many centralization
and standardization efforts have failed, typically because departments
lacked incentives or needed greater local autonomy. While "ownership"
has often been described as the key to providing incentives, these
motivational factors have largely eluded formal characterization.
Using an incomplete contracts approach from economics,
we model the costs and benefits of decentralization, including
critical intangible factors, by explicitly considering the role
of data "ownership." There are two principal contributions
from the approach taken here. First, it provides rigorous mathematical
definitions and a framework for analyzing the incentive costs
and benefits arising from database decentralization. Second, this
theoretical framework leads to the development of a concrete model
and eight normative principles for improved database design. Applications
of this theory are also illustrated through case histories.
Keywords: Database Design, Centralization, Decentralization, Distributed Databases, Ownership, Incomplete Contracts, Incentives, Economic Modeling
Table of Contents
1 Introduction: "Why not one big database?"
Information systems designers sometimes argue that centralized control is better control. From a technology standpoint, this is readily defensible in terms of data integrity and from an economic standpoint in terms of the costs of redundant systems. Fidelity Investments, for example, reduced its costs and improved its data quality and marketing by consolidating customer account data from multiple product lines. Bolstering this view, stories of confusion sometimes characterize decentralization. A Vice President at Johnson and Johnson once waited three weeks for the world-wide list of his top 100 customers due to problems from linking multiple systems. Difficulties with "dis-integrated" systems have led senior staff to inquire "Why not create one big database?" They assume that decentralized systems represent failures in design or, more generously, that designers "did the best they could based on technical limitations of their day." With optical technology and newer microprocessors, barriers imposed by communications bandwidth and speed-bound central hardware continue to fall. Local data control no longer seems necessary or warranted.
Technical constraints, however, represent only part of a more complex story. We present a framework demonstrating that decentralization can be optimal even when there are no technical barriers to complete centralization. This assertion is based on the observation that a system owner has a greater vested interest in the system's success than a non-owner. We examine the extent and importance of this alternative success factor while developing economic guidelines to advance the state of database design. The need for a rational economic approach, as a complement to a technical approach, has been documented by several sources.
Empirically, most centralization and strategic data planning efforts fail to meet expectations (Goodhue, Kirsch, Quillard, & Wybo 1992). Moreover, even after implementing suitable technology, data sharing may never occur. Orlikowski (1992) has observed that an industry standard groupware product, company-wide introduction, and senior management approval were insufficient reasons for employees in a major consulting firm to share information. Culture and incentives opposed the knowledge transfers which the technology was designed to support. In the words of one IS practitioner, "No technology has yet been invented to convince unwilling managers to share information. . ." (Davenport, et al. 1992; p. 56). Information assets have simply become too valuable. In real environments, forces other than technology are also in play.
The issues highlighted by Orlikowski (1992), Davenport (1992) and Goodhue, Kirsch, Quillard, and Wybo (1992) are organizational, not technical. Centralization efforts must look beyond technical concerns to respect the management concerns of the multiple departments they affect. Managers are reluctant, for example, to assign their best technical people to other departments' projects despite it being in the interests of the company as a whole. Ownership of a system and an interest in the benefits accruing from its success, critically affect the incentives of everyone involved; yet motivation issues have previously eluded formalization. It is these incentives which we model here.
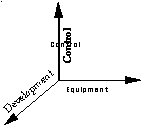
To place centralization and decentralization issues in context, we suggest that centralizing databases involves at least three major dimensions -- equipment, development, and control. These are depicted in Figure 1. In principle, each of these dimensions can be independently centralized or decentralized. As shown in the diagram, the origin represents maximal centralization, whereas moving outward along any given axis represents increased decentralization. Two of these dimensions, equipment and development, have already received attention from several important contributions to the research literature Barghouti, 1991 #129; Bernstein, 1981 #130; Ceri, 1984 #45; Codd, 1970 #3; Date, 1990 #16; Tanenbaum, 1981 #131; Stallings, 1984 #132; Martin, 1982 #142; Kawell, 1988 #133; Chen, 1976 #14; Kreuger, 1992 #135; Notkin, 1987 #143; Siegel, 1991 #57. This paper focuses on unaddressed issues of control.
Figure 1 -- Of the three main axes to decentralization, we focus on control.
Equipment: All computing and data storage equipment can be centralized at one location, with world-wide access provided via remote terminals, such as an automatic teller machine (ATM) network. Alternatively, the computing and data storage equipment can be decentralized. For example, a global brokerage firm might provide a powerful workstation to each of its traders - but each workstation might run exactly the same software that was programmed by a central group. Technical issues of network protocols covering modular design and layering of abstraction levels are summarized in Stallings (1984) and in Tanenbaum (1981). Additional issues of concurrency control covering serializability, record locking, and recovery are also described in Barghouti, 1991 #129, and Bernstein, 1981 #130.
Development: Development may be performed by a central group or by each of the individual groups regardless of whether the equipment is centralized or decentralized. Here, there are a number of diverse contributions. For specific issues of relational database design and data manipulation, references include Date (1981), Ceri (1984), and for strategic data planning, Martin (1982). Issues of cooperative software development are covered in Kawell, Beckhardt, Halvorsen, Ozzie, & Greif (1988). Improving development through software reuse is described by Kreuger (1992). For data integration, there are contributions by Chen (1976) and Shuey (1986), while for semantics of integration there are articles by Siegel (1991) and Notkin (1987).
Control: Control of the databases, planning, and application programs may be centralized to a corporate data center that "owns" the system irrespective of equipment location. Traditionally, this has been the finance department or a corporate resource center. Local divisions would then defer to this central authority for all IS functions. Alternatively, control might be decentralized to local divisions. Under decentralized control, divisions might contract via a "chargeback" system for data center resources and software development or they might assume completely independent responsibility for their IS resources. Each of these options has been observed in practice.
Setting aside the location of equipment and development, we consider control to be centralized if a corporate data center retains the right to make any decision not explicitly and specifically delegated to others. Adopting Grossman and Hart's (1986) use of terminology, we refer to this as the "residual right of control" and associate it with ownership of the system.
For databases, "ownership" and "use" are not easily distinguished concepts. Their connotations convey a variety of privileges from read and query access to creation and modification rights. By usage rights, we mean the ability to access, create, standardize, and modify data as well as all intervening privileges. Usage, however, is not what is meant by ownership. We use ownership and the residual right of control, to mean the right to determine these privileges for others. The archetype is a single database owned and operated by a single department with no outside access. This group, which exercises control over format, access, standards, etc., is the exclusive owner and may then grant successively more permissive access to outsiders until the effective usage privileges of outsiders resemble the usage rights of the owner. It is the authority, however, to subsequently alter or retract these privileges that distinguishes the owner from a non-owner. If the ability to alter others' access is interfered with or vetoed, perhaps by a central authority, then the original owner is not, by our definition, the sole owner of the database. This research addresses the questions of "who should own the data and when should ownership be shared". Eight design principles provide guidelines for deciding on system ownership.
Other researchers have considered ownership as a database design issue. In developing an "interaction theory" of people and systems, Markus Markus, 1983 #115 observes that problems with a database at a large chemical company arose from differences in control: "After FIS [the financial information system] ... all financial transactions were collected into a single database under the control of corporate accountants. The divisional accountants still had to enter data, but they no longer owned it."[1] Similar arguments are put forth by Maxwell Maxwell, 1989 #145 and Wang Wang, 1993 #134. Of the factors Maxwell considers most important to improving data quality, data ownership and origination are among the most critical.[2] Spirig argues that when data ownership and origination are separated, information systems cannot sustain high levels of data quality.[3] The CEO of Johnson and Johnson states unambiguously, "We believe deeply in decentralization because it gives a sense of ownership."[4] The key reason for the importance of ownership is self-interest. Just as rental cars are driven less carefully than cars driven by their owners, "feudal" databases -- those not owned by their users[5] -- are maintained less conscientiously than databases maintained by their owners. The propositions which follow build upon this basic insight and create a rigorous framework for addressing who should control a database system.
The simple insight that ownership provides a better incentive than non-ownership is developed into two separate contributions. First, a rigorous model gives mathematical definitions of non-technical costs and benefits arising from database decentralization. It formalizes the intuitive concepts of ownership, standardization and intangible effort costs that affect system design and that have generally eluded precise specification. The results are therefore testable and less ambiguous. Second, we use the model to construct normative database solutions to problems arising from the separation of ownership and use. This leads us to propose eight database design principles based on ownership to complement the existing design principles based on technology.
Section two explains the economic model. It defines the mathematical concepts and the assumptions used to construct the database design principles. Following these formulation arguments, section three discusses the role of ownership given complementarities among databases and given critical or indispensable personnel. Section four deals with the effects of ownership in the context of database standards and the decision to outsource design and maintenance. This is followed by section five which examines tradeoffs among conflicting design principles and proposes a solution to a lack of ownership incentives in decentralized systems. Throughout each of these five sections, case histories provide context and interpretation in order to simplify the application of the model to real world database design.
2.1 Background: Incomplete Contracts
Incomplete contracts theory, under a basic economic interpretation, considers asset allocation as a cause for firms' integration. Firms should either integrate or divest assets by considering how ownership of these assets affects incentives for the creation of value. When owning an asset induces higher investment and higher realized value, a company should purchase that asset and manage it internally. But when an asset requires no initial investment or it creates greater value in the hands of others, a company may be better off contracting for that asset from the market. Then it should not own that asset. In the present context, the incomplete contracts model is useful in deciding which distribution of database control maximizes database value. A database partition which creates greater value in the hands of one group should be owned by that group rather than another.
Grossman and Hart (1986) and Hart and Moore (1990) consider the effects of ownership on investment behavior and define ownership as the residual right to control access to an asset. The "residual" control rights become important to the extent that specific rights have not been contractually assigned to other parties. If a contract were to completely specify all uses to which an asset could be put, its maintenance schedules, its operating procedures, associated liabilities, etc. then residual rights of control would have no meaning. All control rights would have been determined by the contract. If, on the other hand, an "incomplete" contract were to fail to anticipate every possible contingency -- a much more plausible situation -- then the residual control provided for by ownership would determine the assets' use in disputed circumstances.
Ownership issues, in fact, arise with considerable frequency. In one continuing case, the Chemical Abstracts Society (CAS) produces a database of chemical compounds with a sophisticated capability for matching one related compound with another. CAS, however, has a small user base, a relatively unsophisticated marketing capability, and limited resources. In contrast, DIALOG Information Services has an enormous user base, sophisticated marketing, and considerable resources. DIALOG serves as a reseller of CAS data but is reluctant to make asset specific investments which might improve the user interface or the marketing of the chemical database because it cannot claim ownership of the data it sells. If DIALOG investments were to substantially increase the value of the CAS database, CAS would be in a position to extract a sizable portion of any increased profits. As owner, CAS could restrict access to the database unless DIALOG agreed to share the incremental profits even if DIALOG were the sole investor in any new project This is the classic hold up problem. As a consequence, DIALOG is less likely to invest than if it owned the data and had no need of sharing its profits.
Momentarily putting aside issues of fairness, this suggests that total asset value would be increased if DIALOG were to own the CAS database. DIALOG would invest up to the product's full potential. On the other hand, there may also be reasons not to shift ownership. If it were true that only CAS's chemically sophisticated staff were capable of making updates and enhancements, then asset value would be maximized by leaving ownership with CAS, thereby preserving CAS's incentives. The point is that different incentive requirements lead to different ownership results. Our model captures these and other tradeoffs for databases inside a company where such allocation decisions are more easily made.
There is a further complication, however, relating to the verification of DIALOG's investment. If DIALOG's contributions were easily and completely documented, then any profit calculations could first reward DIALOG with full cost recovery and thereby secure the company's investment participation. But what if these contributions are intangible or difficult to measure such as brand name equity, executive expertise, strategic positioning, or interface quality? Then DIALOG can never be certain that deploying its assets to benefit CAS products will be in DIALOG's own best interests. DIALOG would be unable to document its contribution and would instead be required to expend resources in costly negotiation -- a situation which changes if DIALOG were to own the database.
In the context of database systems, the inability to verify data quality, adequate standardization, usefulness of interfaces and desirable skill sets makes it difficult to specify these features in advance in any meaningful fashion to developers or system administrators. Intangible, unverifiable and non-measurable phenomena are endemic to information and to information systems. Deprived of measurement instruments, technology solutions handle important issues poorly. Brynjolfsson (1994) argued that these properties make the insights of an "incomplete" contracts approach particularly appealing in this domain and derived a number of properties for information ownership by applying the Hart Moore framework.
In fact, DIALOG did attempt to improve certain elements of the user interface only to find that CAS changed the underlying format to render this impossible. CAS feared losing its more profitable core business to its less profitable resale business while it also feared becoming dependent on a single major distributor. The case is currently under litigation. Under these circumstances, DIALOG has little interest in investing further in the database. Consider, as a further illustration, that DIALOG did invest in providing an interface despite CAS's control of key unspecified parameters of the database. CAS was prohibited by contract from withdrawing its database completely, but exercised a residual right as owner to modify the underlying structure. This did not violate the letter of the existing contract, but it has definite implications for investment incentives. Ownership matters when firms must make asset specific investments. The more specific the assets, the more firms prefer to own the assets in which they invest. If the benefits of investment are subject to hold up problems by owners -- problems which arise from unforeseen events -- non-owners will under invest.
2.2 Methodology -- The Grossman, Hart & Moore Model
Formally, Hart & Moore (1990) model ownership in the following
manner. Let V(S, A|X) denote the total value created by the full
set (or grand coalition) S of agents who control assets A and
have previously chosen to invest X. The grand coalition S of all
individuals I can be broken into any subset s. A single agent
is indexed by i = 1 ... I and makes an investment xi. The coalition
s also controls assets a1, a2,
... an OE A and makes collective investments
X = (x1, x2, ... xI)
at a cost C(X). An ownership map a describes the control s exercises
over its assets written as a(s) = {a1, a2,
... an}. The model covers two consecutive periods.
In the first period agents choose their investment levels; in
the second period they realize the benefits accruing from their
investments, and divide the benefits in proportion to their bargaining
power. Having invested in the first period, value is determined
in the second as a function of the agents in the coalition s 
S and the assets a A they control given their prior decision
to invest x = (xi1, xi2,
... xin), hence for a single coalition the notation
is V(s, a|x). The Hart-Moore model includes the following assumptions,
letting Vi(.) _ (_/_xi)V(.):
Assumption 1: V(s, a|x) 
0, V(.) is
twice differentiable and concave in x.
Assumption 2: Ci(xi) 0, C(.) is twice
differentiable and convex in x.
Assumption 3: Vi(s, a|x) = 0 if i oe s.
Assumption 4: (_/_xj)Vi(S,
A|x) 0 for all j _ i.
Assumption 5: For all subsets[6] a A, s S, V(S, A|x)
V(s, a|x) + V(S\s, A\a|x)
Assumption 6: For all subsets a A, s S, Vi(S,
A|x) Vi(s, a|x)
The first two assumptions are standard in economics implying that value per dollar is decreasing while costs are increasing. This allows the use of first order conditions to locate a unique solution. The third assumption implies that an agent's marginal investment affects only coalitions to which he belongs and no other. In assumption four, one agent's investments are complementary at the margin with those of another. Assumption five implies that groups working together create at least as much value as working apart, while assumption six states that the marginal return on investment increases with the number of other agents and new assets in the coalition. Together, assumptions five and six imply that marginal and total values correlate with one another. The optimal investment levels would then be determined according to the globally efficient levels:
(1) 
Additionally, the model defines a governance structure a which maps from subsets of S to subsets of A delineating assets {a1, a2, ... an} which the coalition controls. This leads to rewriting the value function as V(s, a(s)|x). The level of compensation granted each individual member of the coalition, however, is not the total value V(.) but some portion p(s) of V(.) based on the members in the group s. Following Hart and Moore (1990) the subsequent examples will assume that p(s) is the reduced form probability term from the Shapley value.[7] The intuition behind the Shapley value is that it represents each agent's bargaining power in terms of a percentage of the total value created. Bargaining power varies with value contributed and with assets controlled. Persons who contribute more or who control more assets receive a higher percentage of the benefits.
Despite sharing total value, individual coalition members do not share all their respective costs.[8] Due to a lack of verifiability, some costs are not contractible. Due to unreliable software metrics, or to unknown training and effort levels, or perhaps to unobservable resources, direct costs are assumed to be unverifiable. For any costs that are unverifiable, other groups cannot be directly compensated for them and therefore are not willing to bear them.[9] Continuing the earlier analogy, this is equivalent to assuming that if DIALOG can create $100,000 by investing $x of unverified effort in marketing the database owned by CAS, then it will have no recourse for being directly compensated for the $x of investment. However, it will be able to bargain ex post for half the $100,000 of benefits[10] or $50,000. CAS has the bargaining power to insist on the other $50,000 share. Realizing this, DIALOG will only incur expenses up to a maximum of $50,000 even though any investment less than $100,000 would generate a profit. This result holds so long as DIALOG and CAS cannot write a contract based on the size of DIALOG's investment. Assuming it must share any gross proceeds, the same argument applies to investment by CAS as well. Formally, each agent, acting in his own self interest, chooses to invest according to:
(2) 
p(s)[V(s, a(s)|x)
- V(s\{i}, a(s\{i})|x)] - C(xi)
This states that individuals capture a share of incremental value when they create value through their participation and labor or when they control necessary assets. This share is proportional to the value created with them in the coalition net of the value created without them. We also assume that individuals will invest only to the point at which marginal cost equals marginal benefit (MC = MB _ MV). After taking first order derivatives and using assumption three to reduce the second term, this becomes:
(2a) 
p(s)Vi(s, a(s)|x) = Ci(xi)
Because 
p(s) 
1, this result indicates
that the lefthand side is at most Vi(s, a|x) and therefore each
agent under invests. At an intuitive level, the model combines
three key insights. First, today's actions or investments should
affect tomorrow's payoffs, i.e., V depends on x. Second, since
share rises with assets controlled, asset ownership matters as
an investment incentive. This means that i will invest a smaller
xi if j controls critical asset ai
which is essential to i's final product. Third, since not all
actions can be explicitly measured or anticipated and costs C(xi)
are sunk before V is realized, transferring ownership beforehand
can alter and improve investment incentives. In sum, altering
ownership structure can improve total value. This simple rule
leads to our subsequent propositions.
In this paper, we focus on applying the framework specifically to decentralized databases. Of the following design principles, the first three, which consider only intangible costs, are direct applications of propositions that were proven by Hart and Moore (1990). Although Hart and Moore consider residual rights to be synonymous with firm boundaries, we follow Brynjolfsson (1994) and argue that the concept can also apply to intra-firm database transactions. This is because effective ownership of information rarely accrues to its legal owners, the stockholders of the firm. More realistically various groups within the firm are the de facto owners with residual rights of control that can be transferred by changes in organizational structure or management edict. We subsequently relax their assumption of no tangible costs. Building upon the basic framework, the relaxed program of equations leads to design principles four through eight.
2.1 Effects of Independence and Indispensability
For concreteness, we consider a number of case histories. The following case represents a system whose ownership is concentrated in the hands of a central authority while its input operations are decentralized to satellite groups. The inherent conflict in this organizational structure serves to illustrate several issues of control. Each of the cases presented describe database systems in actual use.
Case I: In 1990, local branches of a national post office forwarded their operating data to a central office for storage and processing. Needing data for their own operations, local managers submitted requests for summary reports to the central office. Differences in data requirements emerged, however, since financial and management accounting needs diverged. Although both the primary users and suppliers of data were local, this centralized arrangement reduced local equipment costs, it facilitated standardization and in many ways it was consistent with Strategic Data Planning (SDP). It also provided the central office with financial accounting information to use in gauging postal efficiency. The central office, however, had little incentive to supply management accounting reports to local branches in a timely manner and, being unable to effectively use the delayed reports, branch offices had little incentive to supply accurate or complete data. Consequently, neither office received sufficiently useful data for its accounting purposes. Also, as a further disincentive to supply accurate data, local branches learned of their internal problems only after the head office had learned of them.[11]
One of the main issues of this case is that the central office provides negligible value to the branch offices in exchange for their operating data. In effect, branches have simply been ordered to produce data according to a given set of standards. This independence of value leads to the proposition below.
Define "value independence" as a marginal product
which is unaffected by access to other agents or their assets
i.e. for all coalitions s S and for all sets of assets
a A
s, {ai}as|X)
_ Vi({i}, {ai}|X)where Vi represents the marginal value contributed by group i. This may be interpreted to mean that marginal value is the same regardless of participation or non-participation by other agents.
Design principle 1: Organizations using databases which are value independent should dispense with joint control.
Proof:[12] Consider group i and assume that it must share the value it creates but cannot measure its intangible costs to the satisfaction of other groups. Then i chooses
(3) 
p(s)[V(s, a(s)|X)
- V(s\{i}, a(s\{i})|X) ] - C(xi)
which, after applying first order conditions, reduces to
(3a) 
p(s)Vi({i}, {ai}|X)
= Ci(xi)
by the definition of value independence. The lefthand side is
at most Vi({i}, {ai}|X) and therefore group
i, who must share its assets, will under invest. By assumption
3, i's investments have no effect on the investments of
any other group j when they are not in the same coalition so j's
incentives are no worse under independent control and value independence.
Under independent control, however, i retains his benefits since
p(s)Vi(.)= Vi(.)
and there is no under investment.
Interpretation: Design principle one requires that there be a cooperative payoff for joint control to be beneficial. The reason the post office database system performs badly is that the group responsible for local operations does not own the data it uses. The solution is to pass control of local partitions to local branches. This would both motivate them to supply more accurate and timely data; it would also eliminate the hold up problem of the central office supplying tardy reports. Design principle 1 also supports established research suggesting that data should be stored closest to its most frequent users Ceri, 1984 #45. Note that while the local branch is independent of the central office, the central office depends on the local branch. Design principle 2 handles this aspect below.
Define an "indispensable" agent, i, as one who is critical to project success in the sense that some asset ai is nonfunctional without the agent. The marginal product of any group without the indispensable agent is unaffected by whether or not they own the relevant asset. Mathematically, Vj(s, a|x) _ Vj(s, a\{ai}|x) if ioes.
Design principle 2: Persons or organizations which are indispensable to the functioning of a database partition should control that partition.
Proof:[13] Consider giving ownership of asset ai to i. As new owner, i's incentives are at least as great as before. For any j the change in incentives is the difference between the new and old control structures with the asset transferred:
(4) 
As ai is useless to j without i, and by assumption 6, the second summation is zero. Group j only benefits from working with both i and ai. If ai were owned by a third party k, however, then j would have had to work with {i, j, k} but this introduces an additional hold-up, lowering j's incentives.
Interpretation: In fact, the local branch data is used to support two distinct functions (1) local operations and (2) central office cost accounting. In both cases, the local office is indispensable and design principle 2 indicates that the local office should own this specific partition. If the central office were also indispensable, there would be a conflict -- a possibility which is addressed in design principles five and eight. The effect of transferring ownership to the local office also supports research which finds that internal rather than external pressure leads to more active user participation and superior database performance (Osborn, Madnick, & Wang, 1989). In general, agents should assume control of decentralized functions for which they are indispensable.
2.2 Effects of Cooperative Payoffs and Complementary Assets
Case II: A major midwestern hospital communicates directly with its independent physicians' clinics via a decentralized information system. The system includes database partitions for patient records at the doctors' offices, pharmaceutical data on inventories and treatment suggestions at the hospital, laboratory test results, and operating room scheduling at the hospital. Additionally, the hospital maintains a database of specialty practitioners for doctor to doctor, hospital to doctor, and doctor to hospital referrals. Parties trade information in both directions.
Define "complementary assets" as assets which have great value together but which have negligible value apart. Mathematically, suppose am, an OE A, then
Design principle 3: Database partitions which are complementary should be controlled together.
Proof:[14] Again, consider the transfer of asset an to a group that already owns complementary asset am . The increase in value is given by
(5) 
As the assets are complementary and considering assumption three, the second summation is zero. There is no loss of investment incentives to the present owner of an due to the transfer. The receiving party, in contrast, has strictly higher incentives to invest indicating a net gain in total welfare. Equivalently, am could have been transferred in the other direction thereby increasing the other party's incentives.
Interpretation: Consider the pharmaceuticals database. It includes partitions both for inventories and for treatment methods, two databases which are strictly complementary. There is little merit in prescribing treatments which are unavailable or in stocking drugs which are outdated treatments. To provide the maximum practical incentive, the data should be controlled by the same agent rather than distributed among multiple agents. The hospital does, in fact, control both databases in this more successful system.
3 The Use of Standards and Outsourcing as Control Issues
3.1 Considering both Contractible and Non-Contractible Costs
For several of the principles which follow, we relax assumptions
of the basic model to extend its scope and to generalize the insights
from theoretical to applied tasks. Specifically, while the preceding
propositions assume that all costs are non-contractible, subsequent
propositions allow costs to be divided into verifiable, contractible
or tangible costs 
(tau) and into
unverifiable, non-contractible or intangible costs 
(iota).[15]
In other words, C(xi, xt)
_ (xt) + (xi)
where the subscript refers to the tangible or intangible choice
of investment and the standard convexity assumptions from section
two apply to both and . Intuitively,
this equation captures the idea that any group can independently
choose its investment behavior regarding actions xt,
which are open to public scrutiny, and regarding actions xi,
which are obscured from view. In effect, tangible and intangible
action choices may be separated as may be decisions regarding
equipment purchases and data quality respectively.
Occasionally, computer standards can be used to simplify or even to circumvent data sharing problems. If data formats and management methods are standardized, it may be possible to communicate more of the associated collection and maintenance costs. Adopting a separable cost function, we address the use of standards below.
Define a "standardized" relative to a "non-standardized"
database as one which has lower marginal costs with respect to
intangible uses, updates, and system modifications. Formally,
letting 
and 
represent the
lower intangible costs of the standardized and higher intangible
costs of the non-standardized systems respectively, this leads
to:
i(xi)
< i(xi)
The definition implies that increased standardization across groups
cause information asymmetries among them to grow less quickly.
Each group can more reasonably anticipate another's costs
of working with the system by virtue of system familiarity. Unfamiliarity
and complexity may be alternate interpretations of this phenomenon
in which communicating detailed knowledge of a product is difficult
but developing knowledge through experience is easier. Standards
lower this barrier. By increasing transferable knowledge and the
associated level of database certainty, standards allow hidden,
unverifiable, and intangible costs (xi)
to increase more slowly. This enables us to derive the following
statements relative to database systems.
Design principle 4: Increasing standardization leads to investment nearer the optimum given shared databases.
Proof: Given that some tangible portion of the investments remain fully observable, the maximization problem becomes
(6) max 
p(s)[V(s, a(s)|xt,
xi) - V(s\{i}, a(s\{i})|xt,
xi) - (xt)]
- (xi)
Equating marginal costs and marginal benefits; then noting that only tangible costs may be included in an ex post contract gives:
(6a) 
(_/_xt)p(s)V(s,
a(s)|xi, xt) = 
(_/_xt)p(s)t(xt)
for tangibles and
(6b) 
(_/_xi)p(s)V(s,
a(s)|xi, xt) = (_/_xi)(xi)
for intangibles.
where, by equation (6a), any given group i has optimal investment
in tangible effort xt while, by equation (6b),
the distortion in intangible investment xi is
proportional to (1-
p(s))i(xi).
According to the definition of standardization, this distortion
is less for a standardized system than for a non-standardized
system. By assumption two it follows that x*
- xi 
-
and investment in the standardized system
is nearer the optimum. Note that for a perfectly standardized
system, i(xi) approaches zero implying
that it has no distortion. The implication for ownership is that
standardization increases the potential for efficient decentralized
control.
Corollary 4A: Increasing standardization does not
lead to more efficient use of unshared resources. In this
case 
p(s) = 1 and there is no distortion
regardless of standardization. The decision to standardize will
depend on the expected integration of future assets within a single
department.
Interpretation: Design principle 4 suggests that the benefits of standardization are only partially due to the decreased costs of connecting multiple resources in an information system --the usual reason given for standardizing platforms and software. An alternate explanation is that standardization increases the shared knowledge of the participants enabling them to assess costs and workload more accurately. Design principle 4 accurately predicts that the patient records which are shared between clinics and the hospital will be standardized. Individual clinics' billing information, however, which doctors do not share with one another -- and which they may be legally barred from pooling -- need not be standardized. Individual billing systems may differ from doctor to doctor.
The increased efficiency of standardizing resources has led many companies to insist on compatibility as a prelude to large scale knowledge sharing initiatives. The premise supporting this requirement is that superior knowledge will allow company managers to make better decisions and that standards ensure the availability of superior knowledge with which to make them. One of the insights of this research model, however, is that the presence of hidden or intangible costs -- be they effort levels, reduced political influence, or the opportunity cost of deploying the best staff -- will alter managers' decisions relative to the optimum. A common misconception is that good standards and a sound technical design will ensure a successful system. This leads to the following proposition.
Define "new data availability" as any newly created value such that value exceeds the case of no new investment or V' > V.
Design Principle 5: No amount of standardization is sufficient to ensure new data availability.
Proof: By assumption two, and the definition of standardization,
intangible costs are bounded and non-decreasing. That is it cannot
be the case that i(xi) < 0. Without
loss of generality, assume for the moment that xt
= 0. As a counter example, then, for any level of standardization
let gross intangible costs exceed the shared value received or
(xi) > 
p(s)V(s,
a(s)|xi, xt). Maximizing,
the group invests nothing in intangible effort xi
and V = V0. Importantly, new data availability
can always be assured by contracting on xt.
Such contracts have no effect, however, on xi
without violating the assumptions that it is non-contractible
and separable from xt. Thus, ceteris paribus,
increased standardization cannot be said to uniformly induce new
data availability.
Interpretation: The IS literature provides strong support for this observation. Technology solutions alone do not provide the local compensation necessary to motivate data sharing. One IS consultant points out that, "As information has become the key organizational 'currency,' it has become too valuable for most managers to just give away.", Davenport (1992) p. 53. A representative sample of this phenomenon is provided in Orlikowski (1992). In this field study, an international consulting firm is observed installing collaborative work software following the realization by senior management that they were not making effective use of information technology to leverage existing knowledge. The established reward system, however, hinged on client billable hours leading to a disincentive to sacrifice one's own billable hours to support those of another or even to learn the software. According to Orlikowski, "... where there are few incentives or norms for cooperating or sharing expertise, groupware technology alone cannot engender [them]." Orlikowski (1992) , p. 363. In this framework, the intangible opportunity costs both of learning the system, in lieu of servicing clients, and the political costs of divulging one's specialized or owned knowledge are left completely unreimbursed. Organizations must acknowledge information ownership and provide incentives that compensate for knowledge transfers.
One option for improving system-wide cost effectiveness is to
outsource system maintenance. The incomplete contracts framework
has important implications for asset ownership here as well. The
primary reason to outsource is to realize savings from lower cost
technologies, lower overhead, or increased economies of scale
with declining unit costs. Let the existing cost structure be
given by (xt)
+ (xi) while the subcontractor, with
whom the group outsources, enjoys lower observable costs for a
total of (xt)
+ (xi). Lower observable costs produce
measurable savings (xt)
- (xt)
> 0. These definitions form the basis of design principle six.
Design Principle 6: Lower cost technologies and reduced overhead are insufficient to justify outsourcing.
Proof: Prior to outsourcing a group faces net benefit function
(7) 
p(s)[V(s, a(s)|xt,
xi) - V(s\{i}, a(s\{i})|xt,
xi) - (xt)]
- (xi)
Following outsourcing, however, the net benefit function using cheaper technology is
(7a) 
p(s)[V(s, a(s)|xt,
xi) - V(s\{i}, a(s\{i})|xt,
xi) - (xt)]
Importantly, the intangible efforts cannot be contracted. Since
the contractor does not own the project, he will try to minimize
his hidden costs. This he can do easily by setting (xi)
= 0 or equivalently xi = 0. It follows that
for all value functions such that V(s, a(s)|0, e) > V(s, a(s)|e,
0) where e > 0 and Vi
> Vt and for all cost functions such that
i (xi) < t(xt)
the first equation provides greater net benefit than the second.
This represents the case where the subcontractor captures none
of the incremental value. Using an alternative Nash bargaining
solution, the subcontractor receives half the incremental value
yielding a maximization function of:
(7b) (1/2)
p(s)[V(s, a(s)|xt,
xi) - V(s\{i}, a(s\{i})|xt,
xi) - (xt)]
- (xi)
which is closer to but still far from optimal for exactly the same reasons as in earlier proofs. The precise interpretation of these conditions yields a decision rule for retaining project ownership.
Corollary 6A: Organizations should retain ownership of projects in which a majority and increasing share of the benefit derives from intangibles. Conversely, if a contractor has lower cost technology, organizations should outsource projects in which a minority and decreasing share of the benefit derives from intangibles. Precise parameters are governed by benefit function specifics.
Interpretation: In the case of the post office, the central office might consider outsourcing local office functions on the basis of lowering cost. The outsourcing contractor would then need to perform local data gathering and to assume responsibility for functions previously performed by the local office. The central office, however, would be in no better position to enforce quality data gathering than before since the intangible aspects of this process are not observable. In fact, since the outsourcing contractor does not make use of the data for its own operations, the contractor might be less interested in data quality than the local office. Cost savings alone may not justify outsourcing. Although the details may be open to question, this interpretation confirms the basic premise that ownership is an important incentive as noted by Markus, Maxwell, and the CEO of Johnson and Johnson.
4 Tradeoffs, Control Problems, and Data Translation as a Solution Alternative
As a matter of practical design, principles may not always agree and designers must balance the most important features of each. Occasions arise when design constraints interact or even contradict one another. One of the points of the model, however, is that disregarding any design principle carries a cost. If principles oppose one another then any design choice must bear the costs of the violated design principle. This point is captured in the following proposition.
Design principle 7: If databases are strictly complementary and more than one agent is indispensable, then the presence of private cost information implies that there is no distribution of database control which induces first best investment.[16]
Proof: Given that assets are complementary, design principle two proves under investment will result unless assets are concentrated in the hands of a single agent. Given that agents are indispensable, design principle three proves under investment unless the assets are controlled by both agents. The contradiction follows immediately.
Interpretation: At the national post office, high level financial accounting functions require a central organizational perspective and universal access. The central office is indispensable to these resources implying that the central office should control them. The complementary data, however, are required from the local branches whose indispensability indicates that they should control these resources. Accordingly, there may exist no globally optimal solution.
The potential frequency of conflicting design principles makes it desirable to characterize the tradeoffs between them. This too, however, is difficult.
Corollary 7A: If databases are complementary and more than one agent is indispensable, then the presence of private cost information implies that precedence ordering of design principles is not possible. By construction it is possible to show that the gains from combining complementary assets (equation 5) may be greater than or less than the losses from depriving an indispensable agent of his asset (equation 4). It follows that transferring one of the complementary assets is, a priori, no more desirable than not transferring it.
The absence of an obvious precedence ordering might be cause for concern were it not for two important considerations. The first is that the need to balance conflicting principles is a fact of normal database design. Capturing the essential conflicts and subtleties of real design dilemmas increases the credibility of any model over others which do not admit to such concerns. The second important point is that data and information are unlike traditional assets insofar as copies are virtually free. Giving data to a second owner does not imply that its original owner must forgo its use. This leads us to design principle eight below which describes one method for circumventing the problems introduced by conflicting ownership principles. For most assets, it would be reasonable to follow the design principle which weighed most heavily in inducing investments while compromising the others as little as possible. Without considering the impact of design principle eight, a reasonable heuristic for balancing principles is to consider which ownership structure contributes most to marginal value and to total value. If this is the same structure then it represents the best choice.
As databases posses unique properties regarding duplication, we relax the assumption of indivisibility of assets for design principle eight. Given that data can be copied at a negligible cost, we define a (perfect) "translator" as software which not only copies data from one owner to another but which also translates from the database format native in one group to the database format native in another. A translator may be thought of as a low cost method of providing a duplicate asset. It may be as trivial as a disk copy or as complex as a translation between different vendors' formats. In practical terms, it has two essential features, namely, that it provide near on-demand read access -- a short delay can simply be factored into its cost -- and that it not materially interfere with the operation of the database by its owner. The purpose of allowing different formats is to permit each group to manifest its needs and skills in updates to the format that it uses. Let the price of a translator be K. Under the proposed definition, each group invests according to
(8) 
p(s)[V(s, A|X) - V(s\{i}, A|X)] - C(xi)
- K
This formulation is identical to the one given in equation two
save that the ownership map a(s) A has been replaced with
the entire set of available assets A and the group incurs the
expense of the translator. It is as if each department "owned"
all assets for the price of K.[17] Translators can restore
the incentives provided by better access as indicated by the following
proposition:
Design Principle 8: The use of a (perfect) translator leads to first best levels of investment.
Proof: The foregoing equation measures total value accruing to a single group. The value to all groups is correspondingly
(9) 
[
p(s)[V(s, A|X)
- V(s\{i}, A|X)] - C(xi) - K]
for each proper subset s S such that |s| < |S|, the
inner terms cancel and the residual fractions on the grand coalition
S sum to one leaving only
(9a) V(S, A|X) - 
C(xi)
- IK
which is the maximum possible value given in the introduction net of the constant term IK. The additional ownership privileges afforded by the translator motivates each group, acting in its own interest, to choose the optimal investment level without direction from a central department.
Interpretation: For each combination of assets, a(s) has given way to A and no group suffers a hold up problem due to inaccessible assets. A straightforward solution to the problem faced by the post office is for the central office to use an immediate access copy or "translation" of branch office data. This returns local incentives to the branch office, inducing higher data quality and superior maintenance. It also enables the central office to perform necessary cost accounting and general ledger functions which require centralization in order to paint a global picture of fiscal health. A translator performs the function of increasing resource availability. The importance of the preceding definition of a translator is that it gives a theoretical limit as to how much one is worth. More specifically, this value is given by corollary 8A.
Corollary 8A: The value of a translator is
(10) V(S, A|X) - 
[
p(s)[V(s,
a(s)|X') - V(s\{i}, a(s\{i})|X')]
where X represents first best levels of investment and X' represents second best levels. This amount must exceed IK, for purchase or development to be worthwhile.
Developing intra-organizational translators can increase value. Fidelity First is an example of such a system which integrates all customer account information from multiple products across all Fidelity's divisions. It may be possible, however, even to develop inter-organizational translators. The Composite Information Systems Tool Kit (CISTK) project at MIT [Madnick, Siegel & Wang 1990] integrates data from Reuters, the MIT alumni database, Dataline, Disclosure, and Finsbury. Queries which require access to different data sets in different native formats can be answered using CISTK. Within an organization, the Composite Information System (CIS) approach allows for the possibility of the central group accessing the local group's data in a non-intrusive manner. This results in minimal cost and disruption to the local group, who continues to accrue the full benefits of local control, while the central group incurs only the costs of linking the system (Siegel & Madnick, 1991). Data update and maintenance costs are not duplicated. Linkage expenses, however, are generally much lower than the benefit of direct access to updated and accurate data. The ability to share information permits multiple users and beneficiaries of a decentralized database without necessarily multiplying the costs.
The emergence of multiple views of a database does introduce the potential for divergent growth. We assume that local groups can modify their local copy but not the original and that a translator may be used to reconcile differences between the two at subsequent dates. Database reconciliation is, by itself, an interesting and difficult problem and is an active area of research in the CISTK project. "Context Interchange," which facilitates database transformations and addresses the problem of declaring source data meaning, is especially difficult (Siegel & Madnick, 1991). What we attempt to provide with design principle eight is a mechanism to measure a translator's value added.
Design principle eight responds to problems introduced by the foregoing principles. When assets are complementary and agents are indispensable, for example, it may be possible to configure a system via translation in order that assets behave as if they were combined but indispensable agents do not lose control. The end result is a program of design issues spanning value creation, indispensability, complementarity, standards, and outsourcing as they are affected by ownership. Who owns what is a critical concern in the decision to centralize or decentralize a database system. These issues are summarized in table 1.
DP (1) If a database system is independent of other parts of an
organization, a central authority ought not interfere with its
operation, i.e. it should dispense with joint control.
DP (2) Complementarities in database systems should be combined under centralized control wherever possible.
DP (2, 3) The most essential or indispensable department should control a database partition. Given the preceding point, this means that certain departments should absorb responsibility for complementary parts of their systems, for example, a critical end user group may need to perform its own data entry.
DP (4) Standards only increase the efficiency of shared systems. They are irrelevant for standalone systems.
DP (5) Good technology and good standards alone cannot create good data sharing. Technology alone cannot assure data quality or even availability since system designers must provide proper incentives to critical support staff. The higher the fraction of unobserved costs, the more important are these incentives.
DP (6) Lower overhead is not by itself a sufficient reason to outsource. Outsourcing creates greater value only when the verifiable costs are lower and when the unverifiable costs are low. The higher the fraction of observable costs, the more beneficial outsourcing becomes.
DP (7) Conflicting design principles create unavoidable costs because no one principle will always dominate. In such cases, a reasonable heuristic is to consider the investment motivations of the group which contributes both the greatest marginal and the greatest total value.
DP (8) When systems require shared data, the use of translators can mitigate formatting and access problems. Ownership encourages groups to invest in their systems. Translators effectively increase resource availability and reduce hold up problems.
The fundamental point of this research is that ownership matters. Any group that provides data to other parts of an organization requires compensation for being the source of that data. When it is impossible to provide an explicit contract that rewards those who create and maintain data, "ownership" will be the best way to provide incentives. Otherwise, and despite the best available technology, an organization has not chosen its best incentives and the subtle intangible costs of low effort will appear as distorted, missing, or unusable data. Decentralization concerns equipment and development, but it also concerns intangible issues of ownership and control. Effective ownership is defined as the residual right of control and the motivations of a central IS organization differ substantially from those of a local department depending on who controls the database system. These motivations, as well as the technology, affect realized performance. As various ownership structures generate different behavior, only one structure out of many is likely to maximize database value. The eight principles described here help to choose which structure is best.
Enumerating principles for decentralized database design, also begins to make explicit certain basic ideas, which may be implicit in emergent systems, or which may only be internalized by the best practitioners. Evidence provided by the post office case, the chemical company of the Markus study, the groupware implementation project in the Orlikowsky study, and the Strategic Data Planning project in the Goodhue, Kirsch, Quillard and Wybo study suggest that decentralization problems are complex and by no means isolated. Several carefully designed systems have run afoul of incentives only to fall short of expectations. Building upon the work of Hart and Moore, the contributions of this research have been to reinterpret intuitive concepts of value creation, complementarity, and indispensability in database terms and to further elaborate mathematically precise definitions of standardization, outsourcing, and translation. These definitions are then related to a design program for ownership and decentralization and used to interpret several relevant cases.
In all cases where database value can be measured and made explicit, an agreement or contract which details each party's responsibilities and compensation performs as well as redistributing ownership. Much of principal agent theory is predicated on the ability to achieve optimal effort by measuring results. The intangible nature of information, however, frequently renders measurement of results infeasible. and a common theme from information systems literature is that technology assessments alone are insufficient to guarantee system functionality. Key personnel must be given proper incentives to provide support and maintenance. In the absence of an adequate basis for ensuring performance through specific measures, ownership provides an instrument, however blunt, for giving participants the proper incentives.
This model is amenable to other interpretations as well and we are continuing to develop new principles and to adapt it to related areas within information technology. Progress has been made in applying the framework to aspects of subcontracting, joint ventures, and facilities management. Since it considers intangible issues, the framework can be used to address qualitative problems of linking companies over and above hardware, software, and bandwidth concerns. We hope to propose new theories in this area in future research.
The Shapley formula provides an allocation of total value which is proportional to each member's marginal contribution and to his control of the asset pool. These factors represent plausible interpretations of the more intuitive concept of "bargaining power." Given a predetermined investment level x, mathematically this yields:
(11) _(i, s, a|x) = 
p(s)[V(s, a(s)|x) -
V(s\{i}, a(s\{i})|x)]
where
(12) p(s) = 
which says that a person gets the value created by his group net of the value the group creates without his labors or his assets times the likelihood that he joins that group. The Shapley value balances four properties, namely, (1) treatment of all players is symmetric (2) non-contributors receive nothing (3) the division is Pareto efficient and (4) for multiple games, the expected value of the sum is the sum of the expected values. It also accords well with other efficiency concepts such as Nash equilibrium.
Barghouti, N. S., & Kaiser, G. E. (1991). Concurrency Control in Advanced Database Applications. ACM Computing Surveys, 23(3), 269-317.
Bernstein, P. A., & Goodman, N. (1981). Concurrency Control in Distributed Database Systems. ACM Computing Surveys, 13(2), 185-221.
Brynjolfsson, E. (1994). An Incomplete Contracts Theory of Information, Technology, and Organization (Forthcoming, Management Science)
Ceri, S. & Pelagatti, G. (1984). Distributed Databases Principles and Systems. New York: McGraw-Hill.
Chen, P. (1976) The Entity Relationship Model -- Toward a Unified View of Data. T.O.D.S 1(1); 166-193.
Date, C. (1981) An Introduction to Database Systems, Reading, MA: Addison-Wesley.
Davenport, Thomas, Robert Eccles, and Laurence Prusak. (1992) Information Politics. Sloan Management Review, Fall pp. 53-65.
Goodhue, D. L.,Kirsch, L. J.,Quillard, J. A., & Wybo, M. D. (1992). Strategic Data Planning: Lessons from the Field. MIS Quarterly(March), 11-33.
Grossman, S. J., & Hart, O. D. (1986). The Costs and Benefits of Ownership: A Theory of Vertical and Lateral Integration. Journal of Political Economy, 94(4), 691-719.
Hart, O., & Moore, J. (1990). Property Rights and the Nature of the Firm. Journal of Political Economy, 98(6), 1119-1157.
Hart, Sergiu (1987) The Shapley Value in The New Palgrave; Vol 4. New York, NY: Stockton Press, 318-320.
Kawell, L., Beckhardt, S., Halvorsen, T., Ozzie, R., & Greif, I. (1988). Replicated Document Management in a Group Communication System. In Second Conference on Computer-Supported Cooperative Work, (pp. 226-235). Portland, Oregon:
Kreuger, C. W. (1992). Software Reuse. ACM Computing Surveys, 24(2), 131-183.
Madnick, S. E.,Siegel, M., & Wang, Y. R. (1990). The Composite Information Systems Laboratory (CISL) Project at MIT. IEEE Data Engineering, 13(2), 10-15.
Markus, M. L. (1983). Power, Politics, and MIS Implementation. Communications of the ACM, 26(6), 430-444.
Martin, J. (1982) Strategic Data Planning Methodologies. Englewood Cliffs, NJ: Prentice-Hall.
Notkin, D, Hutchinson, N., Sansilo, J., & Schwartz, M. (1987) Heterogeneous Computing Environments: Report on the ACM SIGOPS Workshop on Accommodating Heterogeneity. Communications of the ACM, 30(2) 33-43.
Orlikowski, Wanda, (1992) Learning from Notes: Organizational Issues in Groupware Implementation. ACM Conference on Computer Supported Cooperative Work. Oct. 31-Nov. 4; Toronto, Canada pp. 362-369.
Osborn, C. S.,Madnick, S. E., & Wang, Y. R. (1989). Motivating Strategic Alliance for Composite Information Systems: The Case of a Major Regional Hospital. In Proceedings of the Twenty Second Annual Hawaii International Conference on System Sciences, . Honolulu:
Richmond, W. B.,Seidmann, A., & Whinston, A. B. (1991). Incomplete Contracting Issues In Information Systems Development Outsourcing. Decision Support Systems Journal (forthcoming).
Shuey, Richard & Gio Wiederhold, (1986) Data Engineering and Information Systems. IEEE Computer, Jan. 18-30
Siegel, M., & Madnick, S. E. (1991). Context Interchange: Sharing the Meaning of Data. SIGMOD Record, 20(4), 77-79.
Stallings, W. (1984). Local Networks. ACM Computing Surveys, 16(1), 3-41.
Tanenbaum, A. (1981). Network Protocols. ACM Computing Surveys,
13(4), 453-489.
[1]p. 438. Emphasis is the original author's.
[2]Other issues are accuracy specifications and communication.
[3]Cited in Wang Wang, 1993 #134 p 31.
[4]Emphasis added. "Information Technology: Unleashing the Power", MIT Sloan School of Management videotape series, CISR 1993.
[5]Terminology adapted from Davenport.
[6]Reader's Note: The notation s\{i} is borrowed from set theory and is used to designate the removal of element i from the set s. If i is a set then s\i will be used and if i was not originally contained in the set then this represents a null operation. In conjunction with the ownership map alpha, for example, the expression "[[alpha]](s\{i})" means the collection of assets owned by a group of which i is not a member.
[7]The full function is actually a fractional share [[florin]](i, s, [[alpha]]) which is based on the individual, the membership and on the assets each member controls. For specifics of this function, see the appendix. Any monotonic decision rule will leave the following propositions unaffected, however, so long as payoff is increasing in the control of additional assets and in contributed value.
[8]Ensuing results may be extended to include both shared (contractible) and unshared (non contractible) costs with minor modifications. It does not, however, materially impact the results while it significantly complicates the exposition.
[9]Costs that are verifiable can be directly compensated via a contract. Ownership will not affect such costs and so initially we focus only on unverifiable costs. We explicitly reintroduce verifiable costs with design principle 4.
[10] Letting DIALOG = i, CAS = j, and investment = x, assets controlled by DIALOG and CAS are [[alpha]](i, j) and the full functional form is [[florin]](i, {i, j}, [[alpha]])V({i, j}, [[alpha]]|x) = (1/2)$100,000) = $50,000. More detail on the Shapley value is provided in the appendix.
[11]This case is based on interviews conducted in May-July 1991.
[12]After Hart Moore proposition 10.
[13]After HartMoore proposition 8.
[14]After Hart Moore proposition 6
[15]Earlier design principles would also hold given contractible costs in addition to uncontractible costs but the exposition becomes still more complex.
[16]Hart and Moore `90 prove a stronger version of this statement for firms but use more restrictive assumptions.
[17]Concepts for data sharing also appear in Brynjolfsson (1990)