Despite evidence that information technology (IT) has recently become a productive investment for a large cross-section of firms, a number of questions remain. Some of these issues can be addressed by extending the basic production function approach that was applied in earlier work. Specifically, in this short paper we 1) control for individual firm differences in productivity by employing a "firm effects" specification, 2) consider the more flexible translog specification instead of only the Cobb-Douglas specification, and 3) allow all parameters to vary between various subsectors of the economy.
We find that while "firm effects" may account for as
much as half of the productivity benefits imputed to IT in earlier
studies, the elasticity of IT remains positive and statistically
significant. We also find that the estimates of IT elasticity
and marginal product are little-changed when the less restrictive
translog production function is employed. Finally, we find only
limited evidence of differences in IT's marginal product between
manufacturing and services and between the "measurable"
and "unmeasurable" sectors of the economy. Surprisingly,
we find that the marginal product of IT is at least as high in
firms that did not grow during 1988-1992 sample period as it is
in firms that grew.
I. Introduction
Fueled by price declines resulting from rapid improvements in
several fundamental technologies, business capital stock of "Office,
Computing and Accounting Machinery" has risen from less than
1% of equipment stock to over 5% in only 10 years (1979-1989).
(Bureau of Economic Analysis 1993) . In some sectors, such
as financial services, computers are the predominant production
technology, and even in manufacturing industries, computers have
led to significant changes in the way products are produced and
delivered (Bylinsky 1994) .
Until recently, however, there has been little evidence that computers
have led to increases in output, thus forming the basis for a
"productivity paradox" (see e.g. (Attewell 1993; Brynjolfsson
1993; Wilson 1993) for reviews.) Roach (1987a) drew attention
to the alarming divergence between rapidly growing IT spending
in the service sector and relatively flat productivity. Loveman
(1994) provided more specific evidence of an IT productivity
shortfall. He used the Management of the Productivity of Information
Technology (MPIT) data set which covers 60 business units of large
firms from 1978-1984 to estimate an economic production function
and found that the marginal product of IT could not be distinguished
from zero. Barua, Kriebel & Mukhopadhyay (1991) using the
same MPIT data also found that IT did not appear to be correlated
with performance, but did influence intermediate measures such
as inventory turnover. Morrison & Berndt (1990) analyzed
industry level data (at the 2-digit SIC level) over the period
1968-1986 and found that a dollar spent on information technology
returned only 80 cents on the margin. In a related study (Berndt
and Morrison 1994, in press) , using much of the same data, they
further concluded that "there is a statistically significant
negative relationship between productivity growth and the high-tech
intensity of the capital."
On the other hand, Siegel & Griliches (1991) found that
IT was positively correlated with productivity growth, although
they also found that the Census Bureau data underlying their analysis
was not very reliable. In previous work (Brynjolfsson and Hitt
1994) , we estimated a production function for a large data set
compiled by International Data Group on IT capital and spending
by over 300 of the largest firms in the U.S. economy over the
time period 1988-1992. We found that the gross marginal product
of IT capital and of IS staff spending each substantially exceeded
their reported costs. Lichtenberg (1993) confirmed these results
using these same data as well as data set from an alternated source
(Information Week), and further found that the marginal product
of IT was at least six times as great as the marginal product
of other types of capital, which he argued represented an appropriate
comparison after accounting for depreciation.
Because American firms went through a period of very visible,
and painful, restructuring in the late 1980s, it is tempting to
conclude that these efforts have finally enabled them to realize
the potential productivity benefits of computers. As David (1989)
has pointed out, such a story has historical parallels but on
a much longer time scale: it took decades before American businesses
made the organizational changes needed to reap the productivity
pay-off from the electric dynamo. However, given the limitations
of both the studies that indicated a productivity shortfall in
the 1970s and early 1980s, and the more recent studies which found
no shortfall in the late 1980s and early 1990s, more evidence
is needed to rule out alternative explanations, such as specification
error in the regressions.
In this paper, we report results of some simple extensions of
previous work which focus on three types of specification errors
which may have affected their results. Potentially the most important
issue is whether the returns to IT are indicative of benefits
to computerization, or simply a marker for firms that are highly
productive for other reasons. A second issue is whether the Cobb-Douglas
functional form used for previous work to estimate the contribution
of computers was overly restrictive leading to a biased estimate
of the elasticity of IT capital and labor. A third issue is whether
pooling data from a large number of different firms blurred differences
between groups of companies with different production processes
such as manufacturing and services, the "measurable"
versus "unmeasurable" sectors of the economy (Griliches
1994) , or firms which grew and those which did not.
To summarize our results:
We find that "firm effects" may account for as much
as half of the productivity benefits imputed to IT in the earlier
studies. Nonetheless, the elasticity of IT remains positive and
statistically significant.
The results are quantitatively similar when the less restrictive
translog production function is employed.
We find only limited evidence of differences in IT elasticity
between manufacturing and services and between the "measurable"
and "unmeasurable" sectors of the economy. Firms which
did not grow between 1988-1992 had no lower estimated elasticity
of IT than firms that did grow.
Our analyses use the same data as that was used in our earlier
work (Brynjolfsson and Hitt 1993; Brynjolfsson and Hitt 1994)
and in the work of Lichtenberg (1993) . However, we depart from
earlier analyses by combining IT capital and IS labor expenses
into a single IT measure. We justify this on the theoretical
grounds that IT capital and labor are complements, and on the
practical grounds that this will enable us to analyze more complex
specifications and subsamples of the original data. As a result,
our findings should provide some insight into the robustness of
the earlier findings to various possible specification errors.
Of course, one significant drawback of our approach is that the
coefficient on IT will no longer reflect purely capital or purely
labor components, and therefore cannot be used to derive a marginal
product that is comparable to the marginal products of either
ordinary capital or ordinary labor.
II. Production Function Framework
Much of the work on the business value of IT, e.g. (Barua et
al. 1991; Berndt and Morrison 1994, in press; Brynjolfsson
and Hitt 1994; Lichtenberg 1993; Loveman 1994) ), and the larger
literature on R&D and productivity (see e.g. (Griliches 1988;
Hall 1993; Mairesse and Hall 1993) ) has used the economic theory
of production to estimate the effects of production inputs on
output. The theory of production states that the inputs a firm
(i) uses can be related to output (Q) via a production function
(F). For our purposes, we will investigate the effect of three
inputs: Computer Capital and Labor (C), Non-computer Capital
(K) and Non-computer Labor (L). In addition to inputs, the production
function may also vary with differences in the industry (j) in
which a firm operates, and differences in time (t) to account
for short-run economic shocks and longer-run disembodied technical
change. Thus we can write:
Q = F (C, K, L; j,t) (1)
The Cobb-Douglas form of the production function allows direct
calculation of output elasticities and can be considered a first
order approximation (in logarithms) to an arbitrary production
function. It is also commonly assumed that time (t) and industry
(j) only result in multiplicative shifts in overall output, but
do not interact with any of the inputs. These assumptions yield
the following equation:
![]() (2)
(2)
where: ![]() = 1 if observation is year t, 0
otherwise
= 1 if observation is year t, 0
otherwise
![]() = 1 if observation is industry j, 0
otherwise
= 1 if observation is industry j, 0
otherwise
By taking logarithms and adding an error term, this equation can be estimated econometrically:
![]() (3)
(3)
In this formulation, the coefficients represent the
output elasticities
of the various inputs, which is the percent change in output for
a 1% change in the quantity of the input. Output elasticities
can also be translated into a marginal product, which is the amount
of additional output provided for an additional dollar of investment
in the input. This equation can be estimated directly for all
firms, thus constraining the output elasticities to be the same
across all types of firms, or targeted to particular subsamples
such as manufacturing or services, which allows estimates of the
output elasticities specific to these sectors.
This paper considers three extensions of this basic framework. The first, is to allow the production function to vary by firm, instead of by industry. While the data is not sufficient to allow all the parameters to vary across firms, we can allow the intercept term (often called multifactor productivity) to vary at the firm level. This accounts for the fact that for reasons exogenous to the model, some firms may be persistently more productive than others. This will prevent us from overstating the contribution of IT in the case where IT investment is also correlated with an unmeasured productivity enhancing characteristic, causing an omitted variables bias. For example, suppose that each firm is endowed with a level of management skill which can lead to higher productivity. Then the "true" production function is:
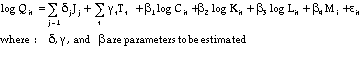 (4)
(4)
where M denotes the management skill. Suppose further that high
performing managers tend to invest disproportionately in IT, so
that there is a positive correlation between M and C. Failing
to account for this effect will lead to an overstatement of the
return to IT since we will be partly measuring the effect of better
management with our IT variable. To the extent that management
skill and other potentially omitted variables can be considered
to be firm characteristics which do not change over the sample
time period, the omitted variables bias will be mitigated by replacing
the sector dummy variable with a dummy variable for each firm
in the data set. Thus, we restate equation 3 with a firm-specific
productivity effect:
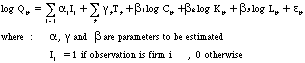 (5)
(5)
This equation can be directly estimated by ordinary least squares,
with a separate dummy variable for each firm. However, there
are a large number of firms (>300) in this sample so this
would require the estimation of over 300 additional dummy variables.
An alternate approach is to find a linear transformation of the
variables in equation 5 that eliminates the firm specific variable
(![]() ) but leaves the other coefficients unchanged.
One such transformation is the "within" transformation
(W) (Greene 1993, pp. 466-469) , defined as:
) but leaves the other coefficients unchanged.
One such transformation is the "within" transformation
(W) (Greene 1993, pp. 466-469) , defined as:
![]() (6)
(6)
where: ![]() is the number of observations of
firm i
is the number of observations of
firm i
Applying the within transformation to equation 5 yields:
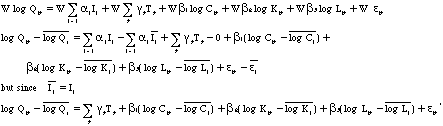 (7a- 7c)
(7a- 7c)
This is the equation desired, where the new error term, ![]() ,
has the usual OLS properties if the error term in equation 5 also
satisfies these properties. This essentially removes the firm-specific
intercept term from the regression in a similar way to removing
the overall intercept term by taking the mean of each variable.
The firm effects can be recovered from this specification by
plugging in the firm mean values to the estimated equation and
calculating the residual from equation 7c.
,
has the usual OLS properties if the error term in equation 5 also
satisfies these properties. This essentially removes the firm-specific
intercept term from the regression in a similar way to removing
the overall intercept term by taking the mean of each variable.
The firm effects can be recovered from this specification by
plugging in the firm mean values to the estimated equation and
calculating the residual from equation 7c.
A second extension is to use a more general functional form such
as the transcendental logarithmic, or "translog", production
function (Christensen and Jorgenson 1969) , which will help minimize
any biases that might result from using the more restrictive Cobb-Douglas
specification. The basic translog function for three inputs
can be written:
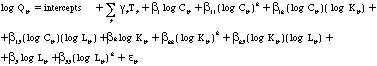 (8)
(8)
where: "intercepts" can vary with by industry or by
firm, in addition to time
The translog production function is an improvement over the Cobb-Douglas
form since it allows the elasticity of substitution to vary by
type of inputs, and allows returns to scale and output elasticity
to vary with the size of the inputs. Conveniently, the Cobb-Douglas
form can be recovered by the translog with various coefficient
restrictions, and thus it is possible to test whether the fit
is improved by employing a more flexible functional form. This
increased flexibility comes at the expense of additional regressors.
Output elasticities can be calculated from the translog estimates
by:
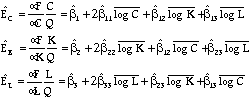 (9a - c)
(9a - c)
Finally, a third extension of the framework is to allow all the
parameters to vary firm certain subsamples of the data. We do
this by running separate regressions for three divisions of the
data set: 1) service firms versus manufacturing firms, 2) firms
in Griliches's "measurable" versus "unmeasurable"
sectors, and 3) firms which had revenue grow versus those with
no revenue growth between 1988 and 1992.
III. Data
The data used for this analysis have been discussed extensively
in a number of papers and therefore will only be briefly discussed
here (see (Brynjolfsson and Hitt 1994) for a detailed description
of this data set and Lichtenberg (1993) for other comments on
the IT spending data utilized in this study). The basic IT spending
data was collected from a survey of central IS departments from
a sample of firms drawn from the top half (by sales) of the Fortune
500 Manufacturing and Fortune 500 Service listings. These surveys,
conducted annually from 1988 to 1992, collect information on the
annual IS budget, the number of desktop machines, such as PCs
and terminals, the amount of the IS budget devoted to labor expenses,
and the market value of the central computer equipment, such as
mainframes, minis and supercomputers. These data were matched
to Standard and Poors' Compustat II, a database of public financial
information, to obtain estimates for firm labor expenses, number
of employees, non-IT capital stock, sales, other expenses and
industry classification. Value-added for each firm was calculated
by subtracting non-labor expenses (calculated as other expenses
less labor expense) from total sales. Deflators from a number
of sources were used to convert the nominal values of the various
inputs and output into constant 1990 dollars to allow inter-year
comparisons on the same basis. A description of the production
input and output variables is shown in table 1.
There are a number of potential problems with the data that could
potentially effect the results. First, because the IT data is
taken from a survey there is potentially a problem of sample selection.
It is possible that the sample is disproportionately comprised
of high performing firms, leading to an upward bias in our estimates.
However, this does not appear to be the case given that the response
rate was high (over 70%), and the sample is not statistically
different than the target population in terms of size, return
on equity, return on sales or return on assets. However, the
target population of the largest Fortune 500 manufacturing and
service firms may somehow be unique. While these firms certainly
represent potentially the largest investors in information technology
equipment, the results may not be generalizable outside this population.
Secondly, and there may be errors in the responses to the survey
questions. In general, the sign of the resulting bias cannot
be determined, although, as discussed in section IV below, in
some special cases one can conclude that the coefficients will
be biased downward (Griliches and Hausman 1986) .
A third problem is that the definition of IT is somewhat narrow,
focusing only on IS Staff, mainframes/large systems and PCs and
does not include other factors such as telecommunications hardware,
peripherals or software which could legitimately be counted as
IT. To the extent that other unmeasured components of IS are
correlated with the measured components in a systematic way for
all firms, our elasticity estimates and standard errors will be
correct, but the marginal product figures will be overstated.
If the "hidden" components are uncorrelated with the
measured component, then the results can be interpreted as applying
only to the included measures of IT and no bias is present in
either the elasticities or marginal products.
A final data problem is that some components had to be estimated.
In order to construct the variable for Computer Capital, we had
to convert the number of PCs and terminals reported by a firm
into a total value. We determined the average value of a PC/terminal
to be approximately $2,835 in 1990, based on data about average
PC prices (Berndt and Griliches 1990) , the composition of PCs
and terminals (IDC 1991) , and an estimated value for a terminal
(Pelaia 1993) . However, our previous work suggests that the
actual results are not particularly sensitive to the choice of
this value (Brynjolfsson and Hitt 1994) . For some firms we also
had to estimate labor expense from number of employees based on
average wages in the particular sector. As before, the results
do not appear to change much when employees are used as the labor
represent potentially the largest investinput variable rather than labor
expense.
While the real quantities of IT used by firms has grown dramatically
over the last few years, it still represents a relatively small
portion of overall inputs in for most firms (Oliner and Sichel
1994) , including those in our sample. Computer capital stock
represents approximately 2% of gross sales, and annual IS labor
expenditures represent on the order of 1% of gross sales. As
Griliches (1994) points out, this, combined with poor output measures
and deflators, makes it difficult to "find the needle in
the haystack" which distinguishes the contribution of IT
from stochastic events that affect the production characteristics
of firms. As a result, although earlier research (Brynjolfsson
& Hitt, 1994; Lichtenberg, 1993) reported statistically significant
contributions to output by both computer capital and information
systems labor in a Cobb-Douglas formulation, more detailed analyses
were not possible. One way to increase the size of the IT effect
is to examine an aggregate IT variable which includes both computer
capital and information systems staff labor. Indeed, it is likely
that the majority of IS labor expenditures are employed to produce
software, a capital good.
However, the two variables cannot be directly added since computer
capital is a stock variable, representing an accumulation of spending
over time, while IS staff is a flow variable representing a single
annual expenditure. To create a stock variable combining the
two, we made two assumptions: that current IS staff spending
is a good estimate of IS spending in the recent past, and that
IS staff "stock" depreciates fully in three years.
Using these assumptions, an IT stock variable is constructed that
equals the sum of IT capital and three times IS labor. This approach
to capitalization of stock is based on that employed by the R&D
accounting literature (Hall 1993) that creates an R&D stock
out of an annual flow and was also the approach used by Loveman
(1994) to calculate IT stock. Because the results could potentially
be sensitive to the assumed life of IS Staff "stock",
we recalculated the basic regression varying the assumption from
1 year to 7 years, and generally find that the elasticity of this
term is relatively stable over this range (.10 to .11), although
marginal product varies as the factor share varies (ranging from
70% to 156%).
The variables used in the analysis are summarized in table 2 along
with other relevant sample characteristics.
IV. Results
Firm Effects
The production function estimates that include industry dummy
variables (industry effects, but no firm effects), are shown in
the Cobb-Douglas form in table 4a, column 1. The comparable regression
with individual firm effects, is shown in column 2. These analyses
represent a regression of Value Added against three inputs, IT
stock, Non-IT Capital, and Non-IT labor, with dummy variables
for each firm (that appears in at least two years), and for time.
Note that the restriction of requiring at least two data points
per firm reduces the sample size slightly, and results in a sample
where the average firm is about 3% larger (table 2).
In the Cobb-Douglas formulation, the elasticity of IT stock drops
from .109 without firm effects to .0495 when firm effects are
accounted for. All coefficients in the regressions are statistically
significant at the .01 level or greater in both specifications.
Even accounting for individual firm productivity differences,
IT makes an important contribution to firm output. These estimates
imply that roughly half of the elasticity of IT is attributable
to individual firm effects, while the remaining are attributable
to the pure effect of IT spending. The elasticities for the other
capital is not significantly affected by the inclusion of firm
effect, although the labor's output elasticity does drop somewhat.
Because the factor share of IT, including both computer capital
and capitalized IS labor spending was .0935 in this sample, firm
effect estimates imply a marginal product for IT stock of approximately
53%. This marginal product estimate is gross of depreciation,
taxes and other costs, but is after accounting for inflation.
We conducted Hausman specification test to examine whether including
firm effects reduces the bias on the other coefficients. The
Hausman test solidly rejects a random effects model with sector
dummy variables, which is consistent with the observation that
the coefficients change substantially when firm effects are included.
Translog Specification
The analysis is repeated in the translog form in table 4a, columns
3 and 4, and elasticities (calculated using equations 9a-c) and
the relevant standard error estimates are shown in the table.
The set of parameters for the translog estimates are also presented
in table 4b. While the estimated elasticities are comparable
to the Cobb-Douglas estimates, the individual coefficients show
a considerable amount of variation and have high standard errors.
We are therefore hesitant to over interpret the translog results
relating to substitution elasticities, and therefore focus primarily
on output elasticities. In this analysis, the elasticity of IT
stock drops from .0815 to .0461 when firm effects are added.
Nonetheless, even in the translog firm-effects specification,
which demands much of the data, we are able to strongly reject
the hypothesis that the return to IT stock is zero (p<.01).
In the basic translog form, the elasticities of non-IT factors,
Capital and Labor, are comparable to the Cobb-Douglas estimates,
however in the firm effects equation, the elasticity of Non-IT
capital is changed substantially - this appears to be a result
of the multicollinearity between Capital and Capital-squared which
have a simple correlation of over .98. However, a Wald test of
the Cobb-Douglas restrictions is rejected for both the firm effects
and industry effects specification, which indicates that the translog
provides a better fit
Overall, this analysis shows that while firm effects can account
for some of the differences in the IT elasticity estimates among
firms, IT stock still makes an economically and statistically
significant contribution to the output of firms in our sample.
This result is robust to the use of a more flexible functional
form, the translog, and therefore cannot be attributed to a spurious
correlation created by an overly restrictive specification. As
before, a Hausman test rejects the random effects plus sector
dummy variables in favor of firm effects.
Interestingly, the finding of significant firm effects for IT,
suggests that in addition to its direct effect, IT may also be
a "marker" for some unspecified variables or strategies
which also increase firm productivity. Specifically, our results
are consistent with the argument by David (1989) and Scott Morton
(1991) that achieving the full productivity impact of computers
requires fundamental changes in many aspects of firms which can
take years to implement. For instance, IT is considered an important
component of "modern manufacturing" strategy, which
includes a cluster of practices and technologies which are purported
to increase productivity (Milgrom and Roberts 1990) , is often
more broadly associated with new organizational strategies and
structures (Malone 1987) .
These results must be interpreted with caution. One reason is
that the use of firm effects tends to magnify the impact of errors
in variables, which can bias the coefficients (Greene 1993) by
the same process that increases errors in variables bias when
using first differences (Griliches and Hausman 1986) . Although,
in general, the direction of errors in variables bias in multivariate
regression is indeterminate, there is a negative bias on all coefficients
if the following two assumptions hold: 1) the regressors are
orthogonal to each other, and 2) the errors in measurement are
uncorrelated between observations and between input variables.
These first of these conditions holds approximately for our data
set: the regressors in the fixed effects specification have correlations
between -.05 and .1. The second condition may also hold because
the various input variables (IT, Capital, Labor) were drawn from
different sources, although by definition, these relationships
cannot be observed. Furthermore, while the firm effects approach
can mitigate the problem of simultaneity (Griliches 1979) , it
does not necessarily eliminate it, so the IT coefficient may still
reflect some lingering effects running from changes in demand
in a particular firm in a particular year to changes in IT investment
in the firm that year.
Differences Among Sectors.
Another weakness of earlier work with the IDG data is that the
estimates did not account for differences in the production processes
between firms operating in different industries, but rather sought
to fit them all with the same functional form, allowing only the
constant term to vary between sectors. While our use of value-added
rather than sales should help to make the production process of,
say, a retailing firm more comparable to a manufacturing firm,
we find that there are substantial differences in the factor composition
between economic sectors, which suggests that they may have different
production functions (table 3).
Three subsamples are considered for this analysis based on issues
raised in earlier research on the business value of IT. First,
it has been argued that while productivity improvements are beginning
to appear in the manufacturing sector, the jury is still out for
IT productivity in the service sector where technology is increasingly
important (Griliches 1994; Quinn et al. 1987; Roach 1991) .
To investigate this assertion, we examine separate translog production
functions for manufacturing and services, the results of which
are shown in table 5. Overall, we find that the elasticity of
IT stock is comparable between the manufacturing sector (elasticity
=.0770) and the service sector (elasticity = .0955). When firm
effects were controlled for, the IT elasticities dropped to .0407
in manufacturing and .0475 in services. Using a Chow test, we
cannot reject the null hypothesis that the IT elasticities are
equal for manufacturing and services (t=.9), nor can we reject
the equality of the Marginal Product of IT in the two subsamples
(t=1.0). However, differences in the elasticities of other
production factors do suggest the existence of substantially different
production relationships. For instance, we reject the hypothesis
that capital elasticities in manufacturing and services are equal
(t=7.9 p<.001).
Second, Griliches (1994) has argued that the differences in measured
productivity growth may not be so much the difference between
manufacturing and services, but the differences between sectors
of the economy where output is "measurable" (manufacturing,
mining, transportation and utilities), to those where output is
"unmeasurable" (retail & wholesale trade, financial
services, other services). While the majority of our sample (85%
of observations) falls into Griliches's "measurable"
sector, it is still possible to get usable estimates of the output
elasticities for these two groups. Using the same method described
in the previous paragraph, we find that the IT stock elasticities
are comparable between the two groups, .0679 for measurable sectors
and .0774 for unmeasurable sectors (Chow test for equality, t=.3,
cannot reject equality). As before, the elasticities for other
factors differed substantially, indicating differences in the
overall production process.
The results on different sectors suggests that, despite substantial
problems of output measurement in certain sectors (see e.g. (Griliches
1992) ), the contribution of IT to output may be as high in the
service sector as in the "measurable" manufacturing
sector. Thus, at least for our sample of large firms, IT was
found to be an important contributor to output across all sectors
of the economy. To the extent that our firm-level data for firms
engaged in finance, trade and other services are less subject
to the output measurement problems which undermine industry-level
deflators, our findings lend support to Griliches's hypothesis
that the reported productivity shortfall in these industries may
be more apparent than real. However, these results should be
interpreted carefully, since a relatively small portion of the
unmeasurable sector is included in this analysis, and the analysis
does not include some firms, such as insurance companies, which
do not have financial information comparable to the other firms
in the sample. However, some firms in all sectors of the economy
(including financial services) are represented which provides
an improvement over some of the previous studies that focused
entirely on manufacturing.
A third interesting subdivision of the data is to look at differences
between growing firms and those with no revenue growth over the
sample period. While firms in both groups increased their IT
capital over the sample period (growing firms increased IT capital
stock by 38% per year while non-growing firms increased stock
by 26% per year compared to a price decline for IT of 20% per
year), growing firms have the luxury of being able to add IT spending
without making the tough choices of cutting back on other inputs
such as labor. In contrast, firms with no revenue growth can
only spend more on IT if they spend less elsewhere. A regression
limited to firms with no growth should be less subject to the
bias that would be caused if firms have a propensity to spend
their free cash flow disproportionately on IT. In other words,
such a regression should have less simultaneity bias. We examined
this question by running separate regressions in firm effects
allowing all parameters to vary between the two subsamples.
Surprisingly,
we find that firms that are not growing actually have higher IT
elasticity: .0729 vs. .130 (Chow test for equality rejects, t=2.4,
p<.01) for firms that grew during the sample period when the
sector effects form was used, although the elasticities are essentially
the same when the firm effects (translog) specification is used.
The result that growing firms do not have higher IT elasticities
than shrinking firms does not support the hypothesis that IT gets
a disproportionate share of new spending. Instead, it may be
that other factors, such as labor, are the preferred place to
spend new revenues. This is consistent with contemporaneous arguments
by Mead (1990) that IT investment is driven by competitive challenges
rather than current economic difficulties. Ironically, such a
policy raises the possibility that simultaneity biases down
the IT coefficient. A second explanation notes that the elasticity
estimates reflects the contribution of IT at the margin, not average
returns. If firms that are not growing underinvest in IT, perhaps
because more layoffs would then be required to maintain budget-balance,
then their marginal returns may exceed their marginal (pecuniary)
costs. Finally, the most intriguing explanation is that painful
restructuring, such as that described by David (1989) is required
to bring the full benefits of IT to the bottom line. This is
certainly the conventional management wisdom (Hammer 1990) and
has some academic support as well (Caves and Krepps 1993) . If
so, the fat, happy, growing firms may be the ones who are missing
the opportunity to restructure and thereby are foregoing some
of IT's potential benefits!
V. Summary and Conclusion
The research on the output contributions of IT is still at a relatively
early stage. This paper seeks to address three important gaps
in previous work: the lack of controls for firm effects, the
restrictiveness of the Cobb-Douglas specification, and possibility
that a single production function does not fit firms in all sectors
of the economy.
Our results differ from previous work in a number of important
ways. First, in comparison to the studies that have found no
contributions of computers we employ a larger sample of data,
leading to improved precision of the estimates. Furthermore,
by considering a later time period in which IT investment is an
order of magnitude larger than in most previous studies, and by
aggregating information systems staff and computer capital, the
overall effect is likely to be larger, making it easier to find
the "needle" of IT contribution in the "haystack"
of random measurement error and other exogenous influences on
production.
In comparison to studies that have found a contribution to IT
in firm level data, we make innovations in both data construction
and econometrics. We directly consider a value-added measure
rather than using gross output (Brynjolfsson and Hitt 1994) or
assuming that the inclusion of dummy variables for industries
and years is adequate for interpreting a regression on gross output
as value-added (Lichtenberg 1993) . Our specification also enables
us evaluate the significance of firm effects which partially addresses
the fact that some of the apparent contribution of IT may simply
be a "marker" of firms that are unusually productive
for other reasons, and to examine several subsamples of the data.
Our results indicate that while firm effects are important, the
contribution of IT is large and statistically significant even
after controlling for individual firm differences in multifactor
productivity. Because our method can provide a ranking of firms
by multifactor productivity, an interesting extension would be
to identify common characteristics of the highly productive firms
and thereby examine some of the conventional wisdom regarding
management best-practice. Furthermore, our method assumes that
firm effects are constant over the sample period. Jensen (1986)
and Lichtenberg (1990) have argued that significant changes in
efficiency often accompany changes in management. A natural extension
of the firm effects approach would be to consider different firm
effects for each management regime, to the extent that the data
allow it.
We also find no significant differences in the contribution of
IT when the restrictiveness of using a Cobb-Douglas specification
is relaxed, or between manufacturing and services, or measurable
and unmeasurable sectors of the economy. These results are encouraging
insofar as they imply that inferences based on the simpler Cobb-Douglas
specification and the easier-to-measure manufacturing sector may
also be more broadly applicable. Nonetheless, the hypothesis
that IT's effects are identical for all subsamples of the data
is clearly unrealistic. The most interesting subsamples to explore
in the future may be those based on organizational form and management
strategy. For instance, more direct tests of the efficacy of
less hierarchical structures and the "reengineering"
of business processes as ways to better harness IT's potential
could be very valuable.
Finally, the striking finding that firms that are not growing
appear to have at least equally high IT elasticities as growing
firms does not support the hypothesis that simultaneity between
growth and IT investment is what is driving the high estimates
of IT elasticity in the full sample. This finding is consistent
with previous results using lagged independent variables as instruments
which also found no evidence of simultaneity (Brynjolfsson and
Hitt 1994) . However, unless better firm-level instruments can
be found, the simultaneity question will remain unresolved.
The high IT returns among firms that were not growing also suggest
some intriguing possibilities for future research to see whether
firms facing a crisis are more likely to undertake the restructuring
that may be required to use IT effectively. This has been a common
theme in the recent management literature (Hammer 1990; Quinn
1992) . Indeed, as discussed in the introduction, one of the most
important differences between our sample and those examined in
studies which found little or no contributions from IT may be
the prevalence of restructuring and downsizing in the 1988-92
period.
Table 1: Data Sources, Construction Procedures, and Deflators*
| Series | Source | Construction Procedure | Deflator |
| Computer Capital and Labor | IDG Survey | Equal to Computer Capital plus 3 times IS Staff (see
below).
Computer Capital. "Market Value of Central Processors"
converted to constant 1990 dollars plus value of reported number of PCs
(assuming a constant value of $2,835 in 1990 dollars). IS Staff. Total IS Budget times percentage of IS Budget (by company) devoted to labor expense. Converted to constant 1990 dollars. | Deflator for Computer Systems (Gordon 1993) for Computer Capital portion, Index of Total Compensation Cost (Private Sector) (Council of Economic Advisors 1992) for IS Staff. |
| Non-IT Capital | Compustat | Book Value of Total Property, Plant and Equipment converted
to constant 1990 dollars.
Deflator year based on calculated average age of capital stock (determined from total depreciation divided by current depreciation). Computer Capital (see above) subtracted from this result. | GDP Implicit Deflator for Fixed Investment (Council of Economic Advisors 1992) |
| Labor | Compustat | Number of Employees, as reported | None |
| Labor Expense | Compustat | Labor expense when reported. Otherwise, estimated from average wage for the sector multiplied by number of employees. IS Staff is subtracted from this value. Converted to constant 1990 dollars. | Index of Total Compensation Cost (Private Sector) (Council of Economic Advisors 1992) |
| Value Added | Compustat | Total sales converted to constant 1990 dollars minus non-Labor Expense. | Industry Specific Deflators from Gross Output and Related Series by Industry, BEA (1977-90) where available (about 80% coverage) - extrapolated for 1992 assuming average inflation rate from previous five years. Otherwise, sector level Producer Price Index for Intermediate Materials Supplies and Components. |
Table 2 - Sample Characteristics*
| Production Inputs and Outputs
(1990 Dollars, Five Year Arithmetic Average) | ||||
| Computer Cap. & Labor | ||||
| Non-IT Capital | ||||
| Labor Expense | ||||
| Value Added | ||||
| Number of Observations | ||||
* - The firm effects subsample is restricted to firms with 2 or more observations over the five year sample period.
Table 3 - Full Sample Sector Characteristics*
| Inputs as a Percentage of Value Added
(1990 Dollars, Full Sample, Arithmetic Mean) | ||||
| Sector | ||||
| Mining | ||||
| Non-Durable Manufacturing | ||||
| Durable Manufacturing | ||||
| Trade | ||||
| Transport &
Utilities | ||||
| Financial Services | ||||
| Other Service | ||||
| Total | ||||
Table 4a - Cobb-Douglas and Translog Estimates for the Firm Effects
Subsample. Standard errors are in parentheses.*
|
|
|
| |
| EC (Computer Capital & Labor) |
|
|
|
|
| EK (Non-IT Capital) |
|
|
|
|
| EL (Labor Expense) |
|
|
|
|
| R2 | ||||
| N (total) | ||||
| Durbin-Watson
Statistic |
Table 4b - Detail of Translog Parameter Estimates. Standard errors
are in parentheses.*
Parameter |
|
|
| C |
|
|
| C2 |
|
|
| C*K |
|
|
| C*L |
|
|
| K |
|
|
| K2 |
|
|
| K*L |
|
|
| L |
|
|
| L2 |
|
|
| Dummy Variables |
| |
| R2 | ||
| N | ||
| DW |
Table 5 - Sample Splits - Translog Production Function Estimates
with Sector Effects
Standard errors are in parentheses.*
| Production Function Estimates (full
sample)
(Sample sizes vary because of exclusions unique to each analysis, as described in the text) | ||||||
| EC (Computer Cap. & Labor) |
|
|
|
|
|
|
| EK (Non-IT Capital) |
|
|
|
|
|
|
| EL(Labor Expense) |
|
|
|
|
|
|
| R2 | ||||||
| N (total) | ||||||
| Durbin-Watson
Statistic | ||||||
References
Attewell, P., "Information Technology and the Productivity Paradox", CUNY mimeo (1993).
Barua, A., C. Kriebel and T. Mukhopadhyay, "Information Technology and Business Value: An Analytic and Empirical Investigation", University of Texas at Austin Working Paper (May 1991).
Berndt, E. and Z. Griliches, "Price Indexes for Microcomputers: An Exploratory Study", NBER Working Paper 3378, (1990).
Berndt, E. R. and C. J. Morrison, "High-tech Capital Formation and Economic Performance in U.S. Manufacturing Industries: An Exploratory Analysis", Journal of Econometrics, (1994, in press).
Brynjolfsson, E., "The Productivity Paradox of Information Technology", Communications of the ACM, 35 (December): 66-77, (1993).
Brynjolfsson, E. and L. Hitt, "Is Information Systems Spending Productive? New Evidence and New Results", Proceedings of the 14th International Conference on Information Systems, Orlando, FL, 1993.
Brynjolfsson, E. and L. Hitt, "Paradox Lost? Firm-level Evidence of the Returns to Information Systems Spending", Management Science, (forthcoming): (1994).
Brynjolfsson, E., T. Malone, V. Gurbaxani and A. Kambil, "Does Information Technology Lead to Smaller Firms?", Management Science, 40 (12): (1994).
Bureau of Economic Analysis, U. S. D. o. C., Fixed Reproducible Tangible Wealth in the United States, 1925-85, U.S. Government Printing Office, Washington, D.C., (1993).
Bylinsky, G., "The Digital Factory", Fortune, 92-110, (November 12, 1994).
Caves, R. and M. Krepps, "Fat: The Displacement of Nonproduction Workers from U.S. Manufacturing Industries", Brookings Papers on Economic Activity: Microeconomics, (2): 227-288, (1993).
Christensen, L. R. and D. W. Jorgenson, "The Measurement of U.S. Real Capital Input, 1929-1967", Review of Income and Wealth, 15 (4): 293-320, (1969).
Council of Economic Advisors (ed.), Economic Report of the President, United States Government Printing Office, Washington, (1992).
David, P. A., "Computer and Dynamo: The Modern Productivity Paradox in a Not-Too-Distant Mirror", Center for Economic Policy Research, Stanford, CA (1989).
Gordon, R. J., The Measurement of Durable Goods Prices, University of Chicago Press (for NBER), Chicago, (1993).
Greene, Econometric Analysis, MacMillan, New York, (1993).
Griliches, Z., "Issues in Assessing the Contribution of Research and Development to Productivity Growth", Bell Journal of Economics, 10 (1 (Spring)): 92-116, (1979).
Griliches, Z., "Productivity Puzzles and R&D: Another Nonexplanation", Journal of Economic Perspectives, 2 (4): 141-154, (1988).
Griliches, Z. (ed.), Output Measurement in the Service Sectors, University of Chicago Press, Chicago, (1992).
Griliches, Z., "Productivity, R&D and the Data Constraint", American Economic Review, (March): 1-23, (1994).
Griliches, Z. and J. Hausman, "Errors in Variables in Panel Data", Journal of Econometrics, 31 93-118, (1986).
Hall, B. H., "New Evidence on the Impacts of Research and Development", Micro-BPEA Conference, Washington, DC, 1993.
Hammer, M., "Reengineering Work: Don't Automate, Obliterate", Harvard Business Review, (July-August): 104-112, (1990).
IDC, I. D. C., "U.S. Information Technology Spending Patterns, 1969-1994", IDC Special Report 5368, (1991).
Jensen, M., "Agency Costs of Free Cash Flow, Corporate Finance, and Takeovers", American Economic Review, 323-329, (1986).
Lichtenberg, F., "The Output Contributions of Computer Equipment and Personnel: A Firm Level Analysis", Columbia Business School Working Paper (October 1993).
Lichtenberg, F. R., "Want More Productivity? Kill That Conglomerate", Wall Street Journal, (June, 1990).
Loveman, G. W., "An Assessment of the Productivity Impact on Information Technologies", pp. 84-110 in Information Technology and the Corporation of the 1990s: Research Studies, Allen, T. J. and M. S. Scott Morton (ed.), MIT Press, Cambridge, MA, (1994).
Mairesse, J. and B. H. Hall, "R&D Investment and Productivity Growth in the 1980s: A First Look at the United States and French Manufacturing Sectors", Prepared for the AEA Meetings, Anaheim, CA, 1993.
Malone, T. W., "Modelling Coordination in Organizations and Markets", Management Science, 33 1317-1332, (1987).
Mead, T., "Should a Recession Curb Your Computer Appetite?", Datamation, 128, (December 1, 1990).
Milgrom, P. and J. Roberts, "The Economics of Modern Manufacturing: Technology, Strategy, and Organization", American Economic Review, 80 (3): 511-528, (1990).
Morrison, C. J. and E. R. Berndt, "Assessing the Productivity of Information Technology Equipment in the U.S. Manufacturing Industries", National Bureau of Economic Research Working Paper 3582, (January 1990).
Oliner, S. D. and D. E. Sichel, "Computers and Output Growth Revisited: How Big is the Puzzle?", Brookings Papers on Economic Activity, (2): (1994).
Pelaia, E., "IBM Terminal Prices", personal communication with IBM Representative, 1993.
Quinn, J. B., Intelligent Enterprise: A New Paradigm for a New Era, The Free Press, New York, (1992).
Quinn, J. B., J. J. Baruch and P. C. Paquette, "Technology in Services", Scientific American, 257 (6): (1987).
Roach, S., "Services Under Siege - The Restructuring Imperative", Harvard Business Review, (September-October): 82-92, (1991).
Roach, S. S., "America's Technology Dilemma: A Profile of the Information Economy", Morgan Stanley Special Economic Study (April 1987a).
Siegel, D. and Z. Griliches, "Purchased Services, Outsourcing, Computers and Productivity in Manufacturing", National Bureau of Economic Research Working Paper 3678, (April 1991).
Wilson, D., "Assessing the Impact of Information Technology on Organizational Performance", in Strategic Information Technology Management, Banker, R., R. Kauffman and M. A. Mahmood (ed.), Idea Group, Harrisburg, PA, (1993).