This research has been generously supported by the MIT Center
for Coordination Science, the MIT Industrial Performance Center,
and the MIT International Financial Services Research Center.
We thank Martin Neil Baily, Rajiv Banker, Ernst Berndt, Geoff
Brooke, Zvi Griliches, Bronwyn Hall, Susan Humphrey, Dan Sichel,
Robert Solow, Paul Strassmann, Diane Wilson, three anonymous referees
and seminar participants at Boston University, Citibank, Harvard
Business School, the International Conference on Information Systems,
MIT, National Technical University in Singapore, Stanford University,
the University of California at Irvine and the U.S. Federal Reserve
for valuable comments, while retaining responsibility for any
errors that remain. We are also grateful to International Data
Group for providing essential data. An abbreviated version of
this paper was published in the Proceedings of the International
Conference on Information Systems, 1993, under the title "Is
Information Systems Spending Productive? New Evidence and New
Results".
The "productivity paradox" of information systems (IS)
is that, despite enormous improvements in the underlying technology,
the benefits of IS spending have not been found in aggregate output
statistics. One explanation is that IS spending may lead to increases
in product quality or variety which tend to be overlooked in aggregate
output statistics, even if they increase sales at the firm-level.
Furthermore, the restructuring and cost-cutting that are often
necessary to realize the potential benefits of IS have only recently
been undertaken in many firms.
Our study uses new firm-level data on several components of IS spending for 1987-1991. The dataset includes 367 large firms which generated approximately $1.8 trillion dollars in output in 1991. We supplemented the IS data with data on other inputs, output, and price deflators from other sources. As a result, we could assess several econometric models of the contribution of IS to firm-level productivity.
Our results indicate that IS have made a substantial and statistically significant contribution to firm output. We find that between 1987 and 1991, gross return on investment (ROI) for computer capital averaged 81% for the firms in our sample. We find that the ROI for computer capital is greater than the return to other types of capital investment and that IS labor spending generates several times as much output as spending on non-IS labor and expenses. Because the models we applied were essentially the same as those that have been previously used to assess the contribution of IS and other factors of production, we attribute the different results to the fact that our data set is more current and larger than others explored. We conclude that the "productivity paradox" disappeared by 1991, at least in our sample of firms.
Spending on information systems (IS), and in particular information
technology (IT) capital, is widely regarded as having enormous
potential for reducing costs and enhancing the competitiveness
of American firms. Although spending has surged in the past decade,
there is surprisingly little formal evidence linking it to higher
productivity. Several studies, such as those by Loveman (1994)
and by Barua, Kriebel & Mukhopadhyay (1991) have been unable
to reject the hypothesis that computers add nothing at all to
total output, while others estimate that the marginal benefits
are less than the marginal costs (Morrison & Berndt, 1990).
This "productivity paradox" has alarmed managers and
puzzled researchers. American corporations have spent billions
of dollars on computers and many firms have radically restructured
their business processes to take advantage of computers. If these
investments have not increased the value produced or reduced costs,
then management must rethink their IS strategies. Roach (1987),
who was among the first to identify the productivity shortfall
in the 1980s, is currently more optimistic about the current prospects
for productivity growth because many firms have finally begun
to realize the potential labor savings enabled by IT. However,
because none of the previous estimates of IT productivity were
based on recent data, this hypothesis remains untested.
This study considers new evidence and finds sharply different
results from previous studies. Our dataset is based on five annual
surveys of several hundred large firms for a total of 1121 observations [1]
over the period 1987-1991. The firms in our sample generated
approximately
$1.8 trillion dollars worth of gross output in the United States
in 1991, and their value-added accounted for about 13% of the
1991 US GDP of $4.86 trillion [2]
(Council of Economic Advisors, 1992).
Because the identity of each of the participating firms is known,
we were able to supplement the IS data with data from several
other sources. As a result, we could assess several econometric
models of the contribution of IS to firm-level productivity.
Our examination of these data indicates that IS have made a substantial
and statistically significant contribution to the output of firms
(Figure 1). Our point estimates indicate that, dollar for dollar,
spending on computer capital created more value than spending
on other types of capital. We find that the contribution of IS
to output does not vary much across years, although there is weak
evidence of a decrease over time. We also find some evidence of
differences across various sectors of the economy. Technological
factors also appear to affect returns. For instance, we find that
neither firms which relied heavily on mainframes, nor firms which
emphasized PC usage performed as well as firms that invested in
a mix of mainframes and personal computers (PCs).
For the firms in our sample, we estimate that the gross return
on investment for computers to be over 50% annually. Considering
a 95% confidence interval around our estimates, we can reject
the hypothesis that computers add nothing to total output. Furthermore,
several of our regressions suggest that the return on investment
for computers is significantly higher than the return on investment
for other types of capital. Our findings suggest that if there
ever was a "productivity paradox", it disappeared in
the 1987-1991 period, at least for our sample of large firms.
1.1 Previous research on IT and
productivity
There is a broad literature on IT value which has been recently
reviewed in detail elsewhere (Brynjolfsson, 1993; Wilson, 1993).
Many of these studies examined correlations between IT spending
ratios and various performance measures, such as profits or stock
returns (Dos Santos, Peffers & Mauer, 1993; Harris & Katz,
1988; Strassmann, 1990), and some found that the correlation was
either zero or very low. In interpreting these findings, it is
important to bear in mind that economic theory predicts that in
equilibrium, high computer investors would not, on average, have
higher profitability or stock market returns. Managers should
be as likely to over-spend as to under-spend, so high spending
should not necessarily be "better". Where correlations
are found, they should be interpreted as indicating an unexpectedly
high or low contribution of information technology, as compared
to the performance that was anticipated when the investments were
made. Thus, perhaps counter-intuitively, zero or weak correlations
between the percentage of spending allocated to IT and profitability
would not indicate a low payoff to computers.
To examine the contribution of IT, it is helpful to work within
a well-defined theoretical framework. For instance, Alpar &
Kim (1990) found that methods based firmly on production theory
from economics could yield insights that were not apparent when
more loosely constrained statistical analyses were performed.
The economic theory of production provides a particularly relevant
framework. This theory posits that the output of a firm is related
to its inputs via a production function and that each input should
make a positive contribution to output. A further prediction of
the theory is that the marginal cost of the last unit of each
input should just equal the marginal benefit produced by that
input. Literally hundreds of studies have estimated production
functions with various inputs, and the predictions of economic
theory have generally been confirmed (See Berndt, 1991, especially
chapters 3 and 9, for an excellent review of many of these studies).
The "productivity paradox" is most accurately linked
to a subset of studies based on the theory of production which
either found no positive correlation overall (Barua, Kriebel &
Mukhopadhyay, 1991; Loveman, 1994), or found that benefits fell
short of costs (Morrison & Berndt, 1990). Using a subset of
the PIMS database [3], Loveman (1994) concluded:
"Investments
in IT showed no net contribution to total output," and Barua,
Kriebel and Mukhudpadhyay (1991) found that computer investments
are not significantly correlated with increases in return on assets.
Similarly, Morrison and Berndt (1990) examined industry-level
data using a production function that controlled for changes in
other inputs and found that each dollar spent on "high tech"
capital [4]increased measured output by only 80 cents on the
margin.
Although previous work provides little econometric evidence that
computers improve productivity, Brynjolfsson's (1993) review of
the overall literature on this "productivity paradox"
concludes that the "shortfall of evidence is not necessarily
evidence of a shortfall." He notes that increases in product
variety and quality should properly be counted as part of the
value of output, but that the price deflators that the government
currently uses to remove the effects of inflation do not properly
reflect this value. As a result, inflation is overestimated and
real output is underestimated by an equivalent amount (because
real output is estimated by multiplying nominal output by a price
deflator). In addition, as with any new technology, a period of
learning, adjustment and restructuring may be necessary to reap
its full benefits. Accordingly, he argues that "mismeasurement"
and "lags" are two of four viable explanations (along
with "redistribution" and "mismanagement")
for the collected findings of earlier studies. This leaves the
question of computer productivity open to continuing debate.
Industry-level output statistics have historically been the only
data that are available for a broad cross-section of the economy.
In a related study using much of the same data as the Morrison
& Berndt (1990) study, Berndt and Morrison (1994) conclude,
"...there is a statistically significant negative relationship
between productivity growth and the high-tech intensity of the
capital." However, they also point out: "it is possible
that the negative productivity results are due to measurement
problems...". Part of the difficulty is that industry-level
data does not provide sufficient detail to distinguish firms within
a particular industry which invest heavily in IT from those with
low IT investments. Only comparisons among industries can be made,
yet these comparisons can be sensitive to price deflators used,
which in turn depend on the assumptions about how much quality
improvement has occurred in each industry. Firm-level production
functions, on the other hand, will better reflect the "true"
outputs of the firm, insofar as the increased sales at each firm
can be directly linked to its use of computers and other inputs,
and all the firms are subject to the same industry-level price
deflator.
On the other hand, a weakness of firm-level data is that it can
be painstaking to collect, and therefore, studies with firm level
data have historically focused on relatively narrow samples. This
has made it difficult to draw generalizable results from these
studies. For instance, Weill (1992) found some positive impacts
for investments in some categories of IS but not for overall IS
spending. However, the 33 strategic business units in his sample
from the valve manufacturing industry accounted for less than
$2 billion in total sales, and he notes, "The findings of
the study have limited external validity." (Weill, 1992.)
By the same token, the Loveman (1994) and Barua, Kriebel and
Mukhudpadhyay
(1991) studies were based on data from only 20 firms in the 1978-82
period and derived only fairly imprecise estimates of IT's relationship
to firm performance.
The imprecision of previous estimates highlights an inherent difficulty
of measuring the benefits of IT investment. To better understand
the perceived benefits, we conducted several interviews with managers
which revealed that they focus on five principal rationales for
investing in IT: labor savings, improved quality, greater product
variety, better customer service, and faster response time. In
principle, all of these benefits should be incorporated in the
government price deflators that convert nominal sales to real
output. In practice, the value of many of the benefits of IT,
other than labor savings, are not well captured in aggregate productivity
or output statistics. [5]
Computers represent on the order of 1% of firms' expenses in most
historical data sets. This makes it very difficult to distinguish
the contribution of IT from random shocks that affect productivity.
As Simon (1984) has observed:
In the physical sciences, when errors of measurement and other
noise are found to be of the same order of magnitude as the phenomena
under study, the response is not to try to squeeze more information
out of the data by statistical means; it is instead to find techniques
for observing the phenomena at a higher level of resolution. The
corresponding strategy for economics is obvious: to secure new
kinds of data at the micro level.
A convincing assessment of IS productivity would ideally employ
a sample which included a large share of the economy (as in the
Berndt and Morrison studies), but at a level of detail that disaggregated
inputs and outputs for individual firms (as in Loveman (1994),
Barua et al. (1991), and Weill (1992)). Furthermore, because the
recent restructuring of many firms may have been essential to
realizing the benefits of IS spending, the data should be as current
as possible. Lack of such detailed data has hampered previous
efforts. While our paper applies essentially the same models as
those used in earlier studies, we use new, firm-level data which
is more recent, more detailed and includes more companies. We
believe this accounts for our sharply different results.
As discussed above, Brynjolfsson (1993) presents a number of hypotheses
for explaining the productivity paradox, including the possibility
that it is an artifact of mismeasurement. We consider this possibility
in this paper.
More formally, we statistically test the following hypotheses:
H1) The output contributions of computer capital and IS staff labor are positive;
H2) The output contributions of computer capital and IS staff labor are greater than their costs.
The "productivity paradox" of computers questions whether
these hypotheses are empirically valid.
In our analysis, we build on a long research stream which applies
production theory to determine the contributions of various inputs
to output. [6] This approach uses economic theory to
determine the
set of relevant variables and to define the structural relationships
among them. The relationship can then be estimated econometrically
and compared with the predictions of economic theory. In particular,
for any given set of inputs, the maximum amount of output that
can be produced, according to the known laws of nature and existing
"technology", is determined by a production function.
As noted by Berndt (1991), various combinations of inputs can
be used to produce a given level of output, so a production function
can be thought of as pages of a book containing alternative blueprints.
This is essentially an engineering definition, but business implications
can be drawn by adding an assumption about how firms behave, such
as profit maximization or cost minimization. Under either assumption,
no inputs will be "wasted", so the only way to increase
output for a given production function is to increase at least
one input.
The theory of production not only posits a relationship among
inputs and output, but also posits that this relationship may
vary depending on particular circumstances. Many of these differences
can be explicitly modeled by a sufficiently general production
function without adding additional variables. For instance, it
is common to assume that there are constant returns to scale,
but more general models will allow for increasing or decreasing
returns to scale. In this way, it is possible to see whether large
firms are more or less efficient than smaller firms. Other differences
may have to do with the economic environment surrounding the firm,
and are not directly related to inputs. Such differences are properly
modeled as additional "control" variables. Depending
on prices and desired levels of output, different firms may choose
different combinations of inputs and outputs, but they will all
adhere to the set defined by their production function. The neoclassical
economic theory of production has been fairly successful empirically,
despite the fact that it treats firms as "black boxes"
and thus ignores history or details of the internal organization
of firms. Of course, in the real world, such factors can make
a significant difference and recent advances in the theory of
the firm may enable them to be more rigorously modeled as well.
To operationalize the theory for our sample, we assume that the
firms in our sample produce a quantity of OUTPUT (Q) via a production
function (F), whose inputs are COMPUTER CAPITAL (C),
NON-COMPUTER
CAPITAL (K), IS STAFF labor (S), and OTHER LABOR AND EXPENSES
(L). [7] These inputs comprise the sum total of all spending by
the
firm and all capitalized investment. Economists historically have
not distinguished computer capital from capital, lumping them
together as a single variable. Similarly, previous estimates of
production functions have not distinguished IS staff labor from
other types of labor and expenses. However, for our purposes,
making this distinction will allow us to directly examine hypothesis
such as H1 and H2 above. We seek to allow for fairly general types
of influences by allowing for any type of environmental factors
which affect the industry or business sector (i) in which the
company operates and year (t) in which the observation was made.
[8] Thus, we can write:
Q = F(C, K, S, L; i,t) (1)
Output and each of the input variables can be measured in either
physical units or dollars. If measured in dollar terms, the results
will more closely reflect the ultimate objective of the firm (profits,
or revenues less costs). However, this approach requires that
we account for inflation and the changing prices of different
inputs and outputs over time and in different industries. This
can be done by multiplying the nominal dollar value of each variable
in each year by an associated deflator to get the real dollar
values. This approach also partially accounts for changes in product
quality or variety to the extent that changes in output characteristics
are incorporated into the price deflators.
Some companies will be more efficient than others at converting
inputs to outputs. The amount of output that can be produced for
a given unit of a given input is often measured as the return
on investment of the input. When examining differences in the
returns of a factor across firms or time periods, it is important
to control for the effects of changes in the other inputs to production.
One way to do this is to assume that the production function,
F, has some functional form, and then estimate its parameters.
This approach has been widely applied empirically (Berndt, 1991,
pp. 449-460).
The economic theory of production places certain technical constraints
on the choice of functional form, such as quasi-concavity and
monotonicity (Varian, 1992). In addition, we observe that firms
use multiple inputs in production, so the functional form should
also include the flexibility to allow continuous adjustment between
inputs as the relative prices of inputs change. [9] Perhaps the
simplest
functional form that relates inputs to outputs and is consistent
with these constraints is the Cobb-Douglas specification, variants
of which have been used since 1896 (Berndt, 1991). This specification
is probably the most common one used when estimating production
functions and remains the standard for studies such as ours, which
seek to account for output growth by looking at inputs and other
factors. [10]
Q = ![]() (2)
(2)
In this specification, b1 and b3
are the output elasticity of COMPUTER CAPITAL and information
systems staff (IS STAFF), respectively. [11]If the coefficients
b0
- b4 sum to 1, then the production function
exhibits constant returns to scale. However, increasing or decreasing
returns to scale can also be modeled with the above function.
The principal restriction implied by the Cobb-Douglas form is
that the elasticity of substitution between factors is constrained
to be equal to -1. This means that as the price of a particular
input increases, the amount of the input employed will decrease
by a proportionate amount, and the quantities other inputs will
increase to maintain the same level of output. As a result, this
formulation is not appropriate for determining whether inputs
are substitutes or complements. Other more complicated functional
forms such as the Transcendental Logarithmic, or Translog, formulation
relaxes this restriction. We consider several other functional
forms in section 3.3 and confirm the appropriateness of the Cobb-Douglas
specification for estimating output elasticities.
The remainder of the paper is organized as follows: in section
2, we describe the statistical methodology and data of our study.
The results are presented in section 3. In section 4, we conclude
with a discussion of the implications of our results.
The basic Cobb-Douglas specification is obviously not linear in
its parameters. However, by taking logarithms of equation (2)
and adding an error term (e), one can derive an equivalent equation
that can be estimated by linear regression. For estimation, we
have organized the equations as a system of five equations,
one for each year: [12]
Log Qi,87 = b0 + b1 Log Ci,87 + b2 Log Ki,87 + b3 Log Si,87 + b4 Log Li,87 + e87 (3a)
Log Qi,88 = b0 + b1 Log Ci,88 + b2 Log Ki,88 + b3 Log Si,88 + b4 Log Li,88 + e88 (3b)
Log Qi,89 = b0 + b1 Log Ci,89 + b2 Log Ki,89 + b3 Log Si,89 + b4 Log Li,89 + e89 (3c)
Log Qi,90 = b0 + b1 Log Ci,90 + b2 Log Ki,90 + b3 Log Si,90 + b4 Log Li,90 + e90 (3d)
Log Qi,91 = b0 +
b1
Log Ci,91 + b2 Log
Ki,91
+ b3 Log Si,91
+ b4 Log Li,91 +
e91
(3e)
While each individual equation is based on a cross-section of
the data, by constraining the coefficients on each factor to be
equivalent in different years, time series variation in the data
will also be reflected in the estimates of the system as a whole.
In fact, under the assumption that the error terms in each equation
are independently and identically distributed, estimating this
system of equations is equivalent to pooling the data and estimating
the parameters by ordinary least squares (OLS). However, it is
likely that the variance of the error term varies across years,
and that there is some correlation between the error terms across
years. It is therefore possible to get more efficient estimates
of the parameters by using the technique of Iterated Seemingly
Unrelated Regressions (ISUR). [13]
As equations (3a) - (3e) are written, we have imposed the usual
restriction that the parameters are equal across the sample, which
allows the most precise estimates of the parameter values. We
can also allow some or all of the parameters to vary over time
or by firm characteristics, although this additional information
is generally obtained at the expense of lowering the precision
of the estimates. We will explore some of these alternative specifications
in the results section; however, the main results of this paper
are based on the system of equations shown in (3a)-(3e).
2.3 Data Sources and Variable Construction
This study employs a unique data set on IS spending by large U.S.
firms which was compiled by International Data Group (IDG). The
information is collected in an annual survey of IS managers at
large firms [14]that has been conducted since 1987.
Respondents are
asked to provide the market value of central processors (mainframes,
minicomputers, supercomputers) used by the firm in the U.S., the
total central IS budget, the percentage of the IS budget devoted
to labor expenses, the number of PCs and terminals in use, and
other IT related information.
Since the names of the firms are known and most of them are publicly
traded, the IS spending information from the IDG survey could
be matched to Compustat II [15] to obtain measures of
output, capital
investment, expenses, number of employees and industry classification.
In addition, these data were also combined with price deflators
for output, capital, employment costs, expenses and IT capital.
There is some discretion as to how the years are matched between
the survey and Compustat. The survey is completed at the end of
the year for data on the following year. Since we are primarily
interested in the value of computer capital stock, and the survey
is timed to be completed by the beginning of the new fiscal year,
we interpret the survey data as a beginning of period value, which
we then match to the end of year data on Compustat (for the previous
period). This also allows us to make maximum use of the survey
data and is the same approach used by IDG for their reports based
on these data (e.g. Maglitta and Sullivan-Trainor, 1991).
IDG reports the "market value of central processors"
(supercomputers, mainframes and minicomputers) but only the total
number of "PCs and terminals". Therefore, the
variable for COMPUTER CAPITAL was obtained by adding the "market
value of central processors" to an estimate of the value
of PCs and terminals, which was computed by multiplying the weighted
average value for PCs and terminals by the number of PCs and terminals. [16]
This approach yields roughly equal values, in aggregate, for central
processors ($33.0 Bn) as for PCs and terminals ($30.4 Bn) in 1991.
These values corroborated by a separate survey by IDG (IDC, 1991)
which tabulates shipments of computer equipment by category. This
aggregate computer capital is then deflated by the computer systems
deflator reported in Gordon (1993).
The variables for IS STAFF, NON-IS LABOR AND EXPENSE and OUTPUT
were computed by multiplying the relevant quantity from the IDG
survey or Compustat by a price deflator. IS STAFF was computed
by multiplying the IS Budget figure from the IDC survey by the
"percentage of the IS budget devoted to labor expenses...",
and deflating this figure. NON-IS LABOR AND EXPENSE was computed
by deflating total expense and subtracting deflated IS STAFF from
this value. Thus, all the expenses of a firm are allocated to
either IS STAFF or NON-IS LABOR AND EXPENSE.
Total capital for each firm was computed from book value of capital
stock, adjusted for inflation by assuming that all investment
was made at an calculated average age (total depreciation/current
depreciation) of the capital stock. [17]From this total capital
figure,
we subtract the deflated value of COMPUTER CAPITAL to get
NON-COMPUTER
CAPITAL. Thus, all capital of a firm is allocated to either COMPUTER
CAPITAL or NON-COMPUTER CAPITAL. The approach to constructing
total capital follows the methods used by other authors who have
studied the rate of return to specific production factors using
a similar methodology (Hall, 1990; Mairesse & Hall, 1993).
The firms in this sample are quite large. Their average sales
were nearly $6.2 billion in 1991. In many other respects, they
are fairly representative of the US economy as a whole. For instance,
their computer capital stock averages just over 2% of total sales,
or about $216 million, which is consistent with the capital flow
tables for the US economy published by the Bureau of Economic
Analysis. Similarly, the average IS budget as a share of sales
was very close to the figure reported in a distinct survey by
CSC/Index. A summary of the sources, construction procedure and
deflator for each variable are provided in Table 1, and sample
statistics are shown in Tables 2a and 2b.
There are a number of possible errors in the data, either as a
result of errors in source data or inaccuracies introduced by
the data construction methods employed. First, the IDG data on
IS spending are largely self-reported and therefore the accuracy
depends on the diligence of the respondents. Some data elements
require some degree of judgment -- particularly the market value
of central processors and the total number of PCs and terminals.
Also, not all companies responded to the survey, and even those
that did respond in one year may not have responded in every other
year. This may result in sample selection bias. For instance,
high performing firms (or perhaps low performing firms) may have
been more interested in participating to the survey. Fortunately,
most of the firms in the target group did respond and, as discussed
above, descriptive statistics for the sample appear to be broadly
consistent with data from other sources.
However, the effect of the potential errors discussed above will
probably be small. The information is intended to be published
and therefore the participants have the incentive to diligently
respond to the survey, and we have checked the aggregate values
against other independent sources. We used different, independent
source (Compustat) for our performance measures and for our IT
variables, making it difficulty to "game" the survey.
We also examined whether the performance of the firms in our sample
(as measured by return on equity (ROE)) differ from the population
of Fortune 500 Manufacturing and Fortune 500 Service firms. Our
results indicate that there are no statistically significant differences
between Fortune 500 firms in our sample and those that are not
(t-stat = 0.7), which suggests that our sample is not disproportionately
comprised of "good" or "bad" firms. However,
since the sampling method targets the largest of the Fortune 500
firms, the average firm in our sample is roughly twice as large
as the average Fortune 500 firm. Finally, the response rate of
the sample is relatively high at over 75%, suggesting that firms
are not selectively participating. These factors suggest that
sample selection bias is not driving the results.
Second, there are a number of reasons why IS STAFF and COMPUTER
CAPITAL may be understated, although by construction these errors
do not reduce total capital and total expense for the firm. The
survey is restricted to central IS spending in the U.S. plus PCs
and terminals both inside and outside the central department.
Some firms may have significant expenditures on information systems
outside the central department or outside the U.S. In addition,
the narrow definitions of IS spending employed in this study may
exclude significant costs that could be legitimately counted as
COMPUTER CAPITAL such as software and communication networks.
Furthermore, by including only the labor portion of IS expenses
in IS STAFF as a separate variable (in order to prevent double
counting of capital expenditure), other parts of the IS budget
are left in the NON-IS LABOR AND EXPENSE category. The effects
of these problems on the final results are discussed in the Results
section.
A third area of potential inaccuracy comes from the price deflators.
Numerous authors (Baily & Gordon, 1988; Siegel & Griliches,
1991) have criticized the current methods employed by the BEA
for constructing industry-level price deflators. It has been argued
that these methods fail to fully account for quality change or
other intangible improvements. If consumer purchases are in part
affected by intangible quality improvements, the use of firm level
data should provide some improvement, because firms which provide
quality improvement will have higher sales and can be directly
compared to firms in the same industry.
Finally, the measurement of OUTPUT and COMPUTER CAPITAL input
in certain service industries appeared particularly troublesome.
For financial services, we found that OUTPUT was poorly predicted
in our model, presumably because of problems in defining and quantifying
the output of financial institutions. [18]In the
telecommunications
industry, it has been argued (Popkin, 1992) that many of the productivity
gains have come from very large investments in computer-based
telephone switching gear, which is primarily classified as communications
equipment and not COMPUTER CAPITAL, although it may be highly
correlated with measured computer capital. We therefore excluded
all firms in the financial services industries (SIC60 - SIC69),
and telecommunications (SIC48). [19]
The basic estimates for this study are obtained by estimating
the system of equations (3a)- (3e) by ISUR (see section 2.2).
Note that we allow the intercept term to vary across sectors and
years.
As reported in column 1 of Table 3, our estimate of b1
indicates that COMPUTER CAPITAL is correlated with a statistically
significant increase in OUTPUT. Specifically, we estimate that
the elasticity of output for COMPUTER CAPITAL is 0.0169 when all
the other input are held constant. Because COMPUTER CAPITAL accounted
for an average of 2.09% of the value of output each year, this
implies a gross ROI (increase in dollar output per dollar of capital
stock ) for COMPUTER CAPITAL of approximately 81% per year. [20] In
other words, for every additional dollar of computer capital stock
that a firm has, its output will increase by 81 cents per year
on the margin. [21]
The estimate for the output elasticity for IS STAFF was 0.0178,
which indicates that each dollar spent here is associated with
a marginal increase in OUTPUT of $2.62. The surprisingly high
return to information systems labor may reflect systematic differences
in human capital, [22] since IS staff are likely to have more
education
than other workers. The high return is certainly consistent with
Krueger's (1991) finding that workers who use computers are paid
a wage premium.
The above estimates strongly support hypothesis H1, that the contribution
of IT is positive. The t-statistics for our estimates of the elasticity
of COMPUTER CAPITAL and IS STAFF are 3.92 and 3.38, respectively,
so we can reject the null hypothesis of zero contribution of IT
at the 0.001 (two-tailed) confidence level for both. We can also
reject the joint hypothesis that they are both equal to zero (c2(2)=43.9,
p<.0001).
To assess H2 (that the contribution of IT is greater than its
cost) it is necessary to estimate the cost of COMPUTER CAPITAL
and IS STAFF. After these costs are subtracted from the gross
benefits reported above, we can then assess whether the remaining
"net" benefits are positive. Because IS STAFF is a flow
variable, calculating net benefits is straightforward: a dollar
of IS STAFF costs one dollar, so the gross returns of $2.62 imply
net returns of $1.62. For IS STAFF, we can reject the null hypothesis
that the returns equal costs in favor of the hypothesis that returns
exceed costs at the .05 confidence level (c2(1)=4.4, p<.035).
Assessing H2 for COMPUTER CAPITAL, which is a stock variable,
requires that we determine how much of the capital stock is "used
up" each year and must be replaced just to return to the
level at the beginning of the year. This is done by multiplying
the annual depreciation [23] rate for computers by the
capital stock
in place. According to the Bureau of Economic Analysis, the average
service life of "Office, Computing and Accounting Machinery"
is seven years (Bureau of Economic Analysis, 1987). If a seven
year service life for computer capital is assumed, then the above
gross returns should be reduced by subtracting just over 14% per
year, so that after seven years the capital stock will be fully
replaced. This procedure yields a net return of 67%. However,
a more conservative assumption is that COMPUTER CAPITAL (in
particular
PCs) could have an average service life as short as 3 years, which
implies that the net rate of return should be reduced by 33%.
This would yield a net ROI estimate of 48%. In either case,
we can reject the null hypothesis that the net marginal returns
to computers are zero (p < .01). [24]
An alternative approach to assessing H2 is to consider the opportunity
cost of investing in COMPUTER CAPITAL or IS STAFF. A dollar
spent in either of these areas could have generated a gross return
of over 6% if it had instead been spent on NON-COMPUTER CAPITAL
or a net return of 7% if it were spent on OTHER LABOR AND EXPENSE.
This suggests that the net benefits were not positive unless they
exceeded these returns by a statistically significant margin.
As shown in Table 6, we can reject the hypothesis that the net
ROI for COMPUTER CAPITAL is equal to the ROI for NON-COMPUTER
CAPITAL, assuming a service life of as little as 3 years for COMPUTER
CAPITAL (and none in NON-COMPUTER CAPITAL) at the .05 confidence
level. Similarly, we can reject the hypothesis that IS STAFF generates
the same returns as spending on OTHER LABOR AND EXPENSE (p <
.05).
Our confidence in the regression taken as a whole is increased
by the fact that the estimated output elasticities for the other
factors of production were all positive and each was consistent
not only with economic theory (i.e. they imply a real rate of
return on non-IT factors of 6%-7%), but also with estimates of
other researchers working with similar data (e.g. Hall, 1993;
Loveman, 1994). Furthermore, the elasticities summed to just over
one, implying constant or slightly increasing returns to scale
overall, which is consistent with the estimates of aggregate production
functions by other researchers (Berndt, 1991). The R2
hovered around 99%, indicating that our independent variables
could "explain" most of the variance in output.
Taken together, our results suggest that during the 1987-1991
time period, firms could have created more value if they had spent
more on computer capital and labor and less on non-computer capital
and labor than they actually did. In the conclusion section, we
discuss some reasons why managers may have made decisions which,
with the benefit of hindsight, appear to have been sub-optimal.
First, however, we will further analyze the robustness of our
results.
3.2 What factors affect the rates of return for
computers?
The estimates described above were based on the assumption that
the parameters did not vary over time, in different sectors, or
across different subsamples of firms. Therefore, they should be
interpreted only as overall averages. However, by using the multiple
equations approach, it is also possible to address questions like:
"Has the return to computers been consistently high, or did
it vary over time?" and "Have some sectors of the economy
had more success in using computers?" We respond to these
questions by allowing the parameters to vary by year or by sector.
Economic theory predicts that managers will increase investments
in any inputs that achieve higher than normal returns, and that
as investment increases, marginal rates of return eventually fall
to "normal" levels. This pattern is supported by our
findings for COMPUTER CAPITAL, which exhibited higher levels of
investment (Figure 2) and lower returns over time (Figure 3).
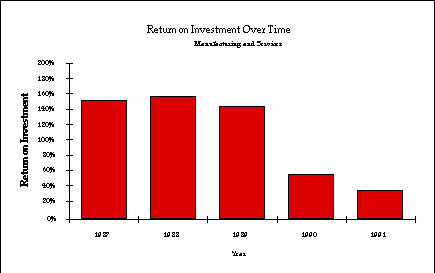
We find that the rates of return are fairly consistent over the
period 1987-1989 and then drop in 1990-1991. We can reject the
null hypothesis of equality of returns over time in the full sample
(c2(4)=11.2, p<.02). However, even at the end of the period,
the returns to COMPUTER CAPITAL still exceed the returns to
NON-COMPUTER
CAPITAL. However, these results should be interpreted with caution
since the composition of the sample changes from year to year
and 1991 was a recession year. [25]
Roach (1987) has argued that the service sector uses computers
much less efficiently than manufacturing and points to aggregate
statistics which report higher overall productivity growth for
manufacturing than for services. Others have argued that aggregate
output in the service sector is poorly measured and this is the
cause of the apparent shortfall of productivity in this sector
(Griliches, 1992). Our data enable us to estimate the contribution
of computers to sales at the firm level, without relying on aggregate
data.
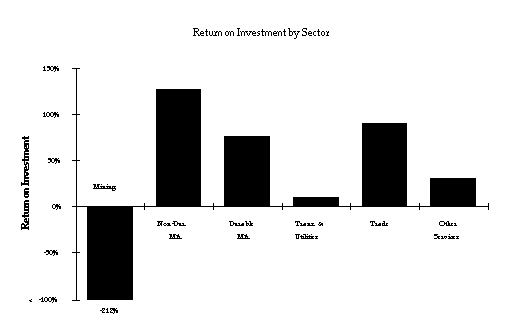
The returns on COMPUTER CAPITAL across sectors are present in
Figure 4. The rate of return (ignoring the mining sector which
includes only 10 firms and has a large standard error) varies
from 10% in transportation and utilities to 127% in durable manufacturing.
The high returns in the two manufacturing sectors may be due to
greater competition, especially from international sources, or
better measurability of the inputs and outputs in these sectors.
While there have been some suggestions that reorganizing service
processes around a "factory" model would help achieve
comparable results in services, we cannot confirm that the differences
in measured returns are due to fundamental differences, or simply
"noise" in the data. Although the returns to computers
in durable and non-durable manufacturing are as high or higher
than the returns in any other sector, we are unable to reject
the hypothesis that these rates of return are the same across
most sectors due to the large standard errors on the coefficient
estimates (without mining, c2(4)=6.6, p<.16).
A second area that can be addressed by our data and method is
technology strategy. We have already shown that firms with more
computer capital will, ceteris paribus, have higher sales
than firms with proportionately less computer capital, but do
the types of computer equipment purchased make a difference?
We have data on two categories of equipment: 1) central processors,
such as mainframes, and 2) PCs and terminals. For this analysis,
we divide the sample into three groups based on the ratio of central
processor value to PCs and terminals. We find that the rate of
return is highest for firms using a more balanced mix of PCs and
mainframes (Table 4), and lower for firms at either extreme. One
interpretation of this finding is that an IS strategy which relies
too heavily on one category of equipment will be less effective
than a more even-handed approach which allows a better "division
of labor".
3.3 Sensitivity Analysis and Possible Biases - Econometric
Issues
Our estimates of the return to COMPUTER CAPITAL required that
a number of assumptions be made about the econometric specification
and the construction of the data set. This section and the following
section explore the validity of our assumptions and generally
finds that the results are robust.
The primary econometric assumption required for ISUR to produce
unbiased estimates of both the parameters and the standard errors
are similar to those for OLS: the error term must be uncorrelated
with the regressors (inputs) and homoskedastic in the cross section.
[26] ISUR implicitly corrects for serial correlation and
heteroskedasticity
over time in our formulation, so that additional restrictions
on the error structure are not necessary. Nonetheless, we computed
single-year OLS estimates both with and without
heteroskedasticity-consistent
standard errors [27] to examine whether heteroskedasticity
is an issue
for the cross-section. The standard error estimates were within
10-20% of each other, indicating that heteroskedasticity does
not appear to be a problem. To test normality of the error terms,
we computed and plotted residuals from the basic specification,
and found them to be roughly normally distributed. It should be
noted that even if these assumptions were violated, the coefficient
estimates (even for OLS) would still be unbiased and consistent,
and therefore represent accurate measures of the contribution
of IT.
However, the third assumption, that the error term is uncorrelated
with the inputs, is potentially an issue. One way in which this
assumption could be violated is if the causality is reversed:
instead of increases in purchases of inputs (e.g. computers) leading
to higher output, an increase in output could lead to further
investment (for example, a firm spends the proceeds from an unexpected
increase in demand on more computer equipment). In this case,
the assumptions for ISUR are violated since the inputs are not
predetermined, and therefore the error term is likely to be correlated
with them. The assumption could also be violated if the input
variables are measured with error [28] (see (Kmenta, 1986)
for a complete
discussion).
Regardless of the source of the error, it is possible to correct
for the potential bias using instrumental variables methods, or
two-stage least squares (2SLS). This method employs instrumental
variables to filter out the endogenous variation and error in
the variables, which then allows consistent estimation of the
parameters. We use once-lagged values of variables as instruments,
since by definition they cannot be associated with unanticipated
shocks in the dependent variable in the following year. [29]
Table
5 reports a comparison of pooled OLS estimates with 2SLS estimates
and shows that the coefficient estimates are similar although
somewhat higher for COMPUTER CAPITAL and lower for IS STAFF. In
both cases the standard errors were substantially larger, as is
expected when instrumental variables are used. Using a Hausman
specification test, we cannot reject the null hypothesis that
the error term is uncorrelated with the regressors (see bottom
of Table 5 for test statistics), and therefore accept our initial
specification.
All the results discussed previously assumed that the production
function was of the Cobb-Douglas form. While this approach is
well grounded in previous research, further insight into the role
of computer capital may be gained by allowing a more flexible
functional form such as the translog. [30]
When we estimated a translog production function, the calculated
value of the COMPUTER CAPITAL elasticity was .0108, [31]which is comparable
to the Cobb-Douglas estimate, although the standard error was
much higher, presumably due to the large number of additional
parameters which had to be estimated. [32] This lends
support to the
assertion made by Griliches (1979) that the choice of functional
form is not critical in the estimation of output elasticities.
3.4 Sensitivity Analysis and Possible Biases - Data Issues
To further explore the robustness of our results, we examined
impact of the possible data errors discussed in section 2.4 that
can be tested: 1) error in the valuation of PCs and terminals,
2) understatement of computer capital, and 3) errors in the price
deflators.
To assess the sensitivity of the results to the assumptions of
the value of PCs and terminals, we recalculated the basic regressions
varying the assumed average PC and terminal value from $0 to $6K.
Note that as the assumed value of PCs and terminals increases,
the increase in COMPUTER CAPITAL will be matched by an equal decrease
in NON-COMPUTER CAPITAL, which is calculated as a residual.
Interestingly,
as shown in Figure 5, the return to COMPUTER CAPITAL in the basic
regression is not very sensitive to the assumed value of PCs and
terminals, ranging from 77% if they are not counted to 59% if
PCs and terminals are counted at $6K. The reason the return rises
at first when PCs and terminals are counted as part of COMPUTER
CAPITAL is presumably that firms with large investments in PCs
and terminals have higher output than similar firms without such
investments. Initially, this increased output raises the estimated
elasticity of COMPUTER CAPITAL by more than the assumed costs
of PCs and terminals, and therefore the estimated return to computers
increases.
Our estimates of the return to COMPUTER CAPITAL or IS STAFF may
be overstated since, as discussed in section 2.3, the true cost
of computer capital and IS staff may be understated. If the hidden
IS costs do not show up elsewhere in the firm, then the effect
on the estimated returns is dependent on how closely correlated
these costs are to our measured COMPUTER CAPITAL. If they are
uncorrelated, our estimate for the elasticity and the return to
COMPUTER CAPITAL is unbiased. If the missing costs are perfectly
correlated with the observed costs, then, because of the logarithmic
form of our specification, they will result only in a multiplicative
scaling of the variables, and the estimated elasticities and the
estimated standard error will be unchanged. [33] For the
same reason,
the sign and statistical significance of our results for the returns
to COMPUTER CAPITAL and IS STAFF will be also unaffected. However,
the denominator used for the ROI calculations will be affected
by increasing computer capital so the estimated ROI will be proportionately
lower or higher. For instance, if the hidden costs lead to a doubling
of the true costs of computer capital, then the true ROI would
fall from 81% to just over 40%. Finally, if the hidden costs are
negatively correlated with the observed costs, then the true returns
would be higher than our estimates.
Another possibility is that the hidden IS capital expenses (e.g.
software) show up elsewhere, such as in the NON-IS LABOR AND
EXPENSE
category. To estimate the potential impact of these omissions,
we estimate the potential size of the omitted misclassified IS
capital relative to COMPUTER CAPITAL using data from another IDG
survey (IDC, 1991) on aggregate IS expenditures, including software
as well as hardware. To derive a reasonable lower bound on the
returns to COMPUTER CAPITAL, we assume that the misclassified
IS capital had an average service life of three years, and further
make the worst-case assumption of perfect correlation between
misclassified IS capital and COMPUTER CAPITAL (and reduce
proportionally
the amount of NON-IS LABOR AND EXPENSE). In this scenario, our
estimates for the amount of COMPUTER CAPITAL in firms roughly
doubles, yet the rates of return are little unchanged from the
basic analysis that does not include misclassified IS capital
(68% vs. 81%). This surprising result appears to be due to the
fact that the return on NON-IS LABOR AND EXPENSE is at least as
high as the return on COMPUTER CAPITAL, so moving costs from one
category to another does not change overall returns much.
It should be noted that the definition of COMPUTER CAPITAL used
in this study was fairly narrow and did not include items such
as telecommunications equipment, scientific instruments, networking
equipment. The findings should be interpreted accordingly and
do not necessarily apply to broader definitions of IT.
One final contribution to error is the understatement of output
due to errors in the price deflators. While it is difficult to
directly correct for this problem, we estimated the basic equations
year by year, so that errors in the relative deflators would have
no impact on the elasticity estimates. The estimated returns ranged
109% to 197% versus 81% when all five years were estimated
simultaneously.
The standard error on the estimates was significantly higher for
all estimates, which can account for the greater range of estimates.
Overall, this suggests that our basic findings are not a result
of the assumed price deflators. However, if the price deflators
systematically underestimate the value of intangible product change
over time or between firms, our measure of output will be understated,
implying that the actual return for computer capital is higher
than our estimates.
On balance, we may have underestimated both IS input and final
output. The directions of the resulting biases go in opposite
directions, but under reasonable assumptions they do not appear
to obviate the basic finding that the return on IS capital and
labor spending is statistically significant and exceeds that of
other types of capital and labor.
4.1 Comparison with earlier research
Although we found that computer capital and IS labor increase output significantly, several other studies have failed to find evidence that IT increases output. Because the models we used were similar to those used by several previous researchers, we attribute our different findings primarily to the larger and more recent data set we used. Specifically, there are at least three reasons why our results may differ from previous results.
First, we examined a later time period, (1987-1991), than did
Loveman (1978-1982), Barua et al. (1978-1982) or Berndt &
Morrison (1968-1986). The massive build-up of computer capital
is a relatively recent phenomenon. Indeed, the delivered amount
of computer power in the companies in our sample is likely to
be at least an order of magnitude greater than that in comparable
firms from the period studied by the other authors. Brynjolfsson
(1993) argues that even if the ROI of IT were twice that of non-IT
capital, its impact on output in the 1970s or early 1980s would
not have been large enough to be detected by conventional estimation
procedures. Furthermore, the changes in business processes needed
to realize the benefits of IT may have taken some time to implement,
so it is possible that the actual returns from investments in
computers were initially fairly low. In particular, computers
may have initially created organizational slack which was only
recently eliminated, perhaps hastened by the increased attention
engendered by earlier studies that indicated a potential productivity
shortfall and suggestions that "to computerize the office,
you have to reinvent the office" (Thurow, 1990). Apparently,
an analogous period of organizational redesign was necessary to
unleash the benefits of electric motors (David, 1989).
A pattern of low initial returns is also consistent with the strategy
for optimal investment in the presence of learning-by-using: short-term
returns should initially be lower than returns for other capital,
but subsequently rise to exceed the returns to other capital,
compensating for the "investment" in learning (Lester
& McCabe, 1993). Under this interpretation, our high estimates
of computer ROI indicate that businesses are beginning to reap
rewards from the experimentation and learning phase in the early
1980s.
Second, we were able to use different and more detailed firm-level
data than had been available before. We argue that the effects
of computers in increasing variety, quality or other intangibles
are more likely to be detected in firm level data than in the
aggregate data. Unfortunately, all such data, including ours,
is likely to include data errors. It is possible that the data
errors in our sample happened to be more favorable (or less unfavorable)
to computers than those in other samples. We attempted to minimize
the influence of data errors by cross-checking with other data
sources, eliminating outliers, and examining the robustness of
the results to different subsamples and specifications. In addition,
the large size of our sample, should, by the law of large numbers,
mitigate the influence of random disturbances. Indeed, the precision
of our estimates was generally much higher than those of previous
studies; the statistical significance of our estimates owes as
much to the tighter confidence bounds as to higher point estimates.
Third, our sample consisted entirely of relatively large "Fortune
500" firms. It is possible that the high IS contribution
we find is limited to these larger firms. However, an earlier
study, (Brynjolfsson, Malone, Gurbaxani & Kambil, 1994), found
evidence that smaller firms may benefit disproportionately from
investments in information technology. In any event, because firms
in the sample accounted for such a large share of the total US
output, the economic relevance of our findings is not heavily
dependent on extrapolation of the results to firms outside of
the sample.
If the spending on computers is correlated with significantly
higher returns than spending on other types of capital, it does
not necessarily follow that companies should increase spending
on computers. The firms with high returns and high levels of computer
investment may differ systematically from the low performers in
ways that cannot be rectified simply by increasing spending. For
instance, recent economic theory has suggested that "modern
manufacturing", involving high intensity of computer usage,
may require a radical change in organization (Milgrom & Roberts,
1990). This possibility is emphasized in numerous management books
and articles (see, e.g. Malone & Rockart, 1991; Scott Morton,
1991) and supported in our discussions with managers, both at
their firms and during a workshop on IT and Productivity attended
by approximately 30 industry representatives. [34]
Furthermore, our results showing a high gross rate of return may
be indicative of the differences between computer investment and
other types of investment. For instance, managers may perceive
IS investment as riskier than other investments, and therefore
require higher expected returns to compensate for the increased
risk. Finally, IS is often cited as an enabling technology which
does not just produce productivity improvements for individuals,
but provides a vast advantage by facilitating business process
redesign or improving the ability of groups to work together.
In this sense, our results may be indicative of the substantial
payoffs to reengineering and other recent business innovations.
We examined data which included over 1000 observations on output
and several inputs at the firm level for 1987-1991. The firms
in our sample had aggregate sales of over $1.8 trillion in 1991
and thus account for a substantional share of the U.S. economy.
We tested a broad variety of specifications, examined several
different subsamples of the data, and validated the assumptions
of our econometric procedures to the extent possible.
The data indicate that COMPUTER CAPITAL and IS STAFF spending
contribute significantly to firm level OUTPUT. Furthermore, we
were able to reject the hypothesis that the (gross) ROI for COMPUTER
CAPITAL was equal to the ROI for NON-COMPUTER CAPITAL in favor
of the hypothesis that the ROI for COMPUTER CAPITAL was higher.
Even when we adjusted for depreciation using the BEA 7-year service
life assumption for COMPUTER CAPITAL, the differences in return
are still significant. The basic result that COMPUTER CAPITAL
and IS STAFF contribute significantly to total output are robust
to reasonable assumptions about measurement error due to exclusion
of unmeasured factors.
There are a number of other directions in which this work could
be extended. In the current formulation, it is difficult to make
direct comparisons between firms in different industries because
the definitions of "output" vary. An alternative dependent
variable which can be estimated using production functions is
value added. This approach should treat firms in a more comparable
way, allowing greater precision in estimating the effects of IS
spending, and therefore enabling more complex production function
relationships to be examined. For instance, comparisons of retail
stores with manufacturing firms will be more accurate when value-added
is used as the dependent variable. It would also be worthwhile
to investigate the role of other variables, such as research and
development expenditures, which might be associated with the
advancement
of technology in general, and IT in particular. One recent study
(Dunne, 1993) suggested that firms which invest heavily in R&D
are also most innovative in their use of IT.
Although our approach allowed us to infer the value created by
intangibles like product variety by looking at changes in the
revenues at the firm level, more direct approaches might also
be promising. For instance, other variables can be collected to
see whether computer productivity is systematically related to
characteristics such as variety of product line, or the average
defect rate in their output.
Finally, the type of extension which is likely to have the greatest
impact on practice is further analysis of the factors which differentiate
firms with high returns to IT from low performers. For instance,
is the current "downsizing" of firms leading to higher
IT productivity? Are the firms that have undertaken substantial
"reengineering efforts" also the ones with the highest
returns? Since this study has presented evidence that the computer
"productivity paradox" is a thing of the past, it seems
appropriate that the next round of work should focus on identifying
the strategies which have led to large IT productivity.
Figure 1: Comparison of Gross Return on Investment
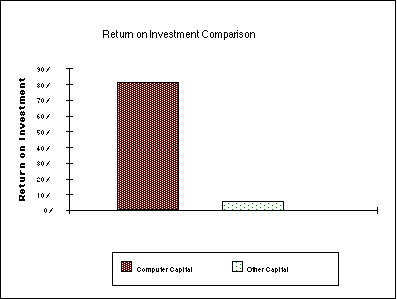
Figure 2: Changes in IT Inputs over Time
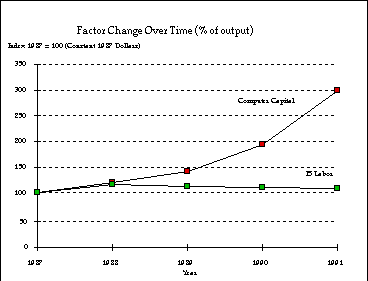
Figure 3: Gross Return on Investment Over Time - Manufacturing
& Services
| 1987 | 1988 | 1989 | 1990 | 1991 | |
| Coefficient | .0177** | .0222*** | .0239*** | .0125** | .0121** |
| Std. Error | (.00721) | (.00646) | (.00657) | (.00574) | (.00594) |
| N | 135 | 133 | 274 | 286 | 293 |
Key: *** - p<.01, ** - p<.05, * - p<.1, standard errors
in parenthesis
Figure 4: Gross Return on Investment by Sector
|
|
| ||||
| Coefficient | ||||||
| Std. Error | ||||||
| N (total) |
Key: *** - p<.01, ** - p<.05, * - p<.1, standard errors
in parenthesis
Figure 5: Gross Return on Investment for Computer Capital with
different PC value assumptions
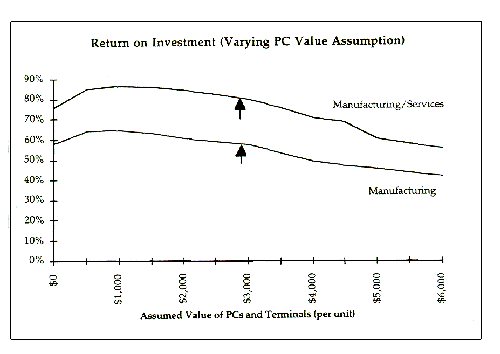
Table 1: Data Sources, Construction Procedures, and Deflators
| Series | Source | Construction Procedure | Deflator |
| Computer Capital | IDG Survey | "Market Value of Central Processors" converted to constant 1987 dollars, plus the total number of PCs and terminals multiplied by an average value of a PC/terminal, also converted to constant 1987 dollars. | Deflator for Computer Systems (Gordon, 1993). |
| Non- Computer Capital | Compustat | Total Property, Plant and Equipment Investment converted to constant 1987 dollars. Adjusted for retirements using Winfrey S-3 Table (10 year service life) and aggregated to create capital stock. Computer capital as calculated above was subtracted from this result. | GDP Implicit Deflator for Fixed Investment (Council of Economic Advisors, 1992). |
| IS Staff | IDG Survey | Total IS Budget times percentage of IS Budget (by company) devoted to labor expense. Converted to constant 1987 dollars. | Index of Total Compensation Cost (Private Sector) (Council of Economic Advisors, 1992). |
| Non-IS Labor and Expense | Compustat | Total Labor, Materials and other non-interest expenses converted to constant 1987 dollars. IS labor as calculated above was subtracted from this result. | Producer Price Index for Intermediate Materials, Supplies and Components (Council of Economic Advisors, 1992). |
| Output | Compustat | Total sales converted to constant 1987 dollars. | Industry Specific Deflators from Gross Output and Related Series by Industry, BEA (1977-89) where available (about 80% coverage) - extrapolated for 1991 assuming average inflation rate from previous five years. Otherwise, sector level Producer Price Index for Intermediate Materials Supplies and Components (Gorman, 1992). |
Table 2a: Summary Statistics
| Sample Statistics - Average over
all points
(Constant 1987 Dollars) | |||
|
|
| |
| Output | |||
| Computer Capital | |||
| Non-Computer Capital | |||
| IS Staff | |||
| Non-IS Labor and Expenses | |||
| Avg. Number of Companies per Year | |||
| Total Observations | |||
Table 2b. Sample Composition relative to Fortune 500 Population
| Sample Composition
Number of firms | |||
|
| ||
| 1991 Sample | |||
| All Firms in Compustat | |||
Table 3: Base Regressions - Coefficient Estimates and Implied Gross Rates of Return
All parameters (except year dummy) constrained to be equal across
years.
| Parameter | ||
| ||
| ||
| ||
| ||
| Dummy Variables |
| |
| R2 (1991) | ||
| N (1991) | ||
| N (total) |
Key: *** - p<.01, ** - p<.05, * - p<.1, standard errors
in parenthesis
Table 4: Split Sample Regression Results
| Coefficient Estimates and Rates
of Return for Each Cell contains coefficient estimate, (standard error), ROI | ||||
Sample Split |
| |||
| Mainframes/PCs Ratio |
|
|
|
|
Key: *** - p<.01, ** - p<.05, * - p<.1, standard errors in parenthesis
1 - Ordering by X 2 tests of return
differences. P-value
shown represents null hypothesis of equality across groups.
Table 5: Specification Test - Comparison of OLS and Two-Stage Least Squares
All parameters (except year dummy) constrained to be equal across
years.
Parameter |
|
|
|
| |
|
| |
|
| |
|
| |
| Dummy Variables |
|
|
| R2 | ||
| N (total) | ||
| Durbin-Watson Statistic |
Key: *** - p<.01, ** - p<.05, * - p<.1, standard errors are in parentheses
Note: OLS estimates are for sample of same firms as were available
for 2SLS regression.
Hausman Test Results (instruments are lagged independent variables):
X 2 (4) = 6.40, (p<.17) - cannot reject exogeneity
Table 6: X 2 Tests for Differences in Rates of Return
between Computer
Capital and Other Capital
| Return Difference Tests | |||
| Gross Return | |||
| Net - 7 Year Service Life | |||
| Net - 3 Year Service Life |
Key: *** - p<.01, ** - p<.05, * - p<.1, two-tailed tests
A significant test indicates that the return on computer capital is greater than the return on other capital.
Alpar, P. and Kim, M. A Comparison of Approaches to the Measurement
of IT Value. In Proceedings of the Twenty-Second Hawaii International
Conference on System Science (Honolulu, HI, 1990).
Baily, M.N. and Gordon, R.J. The Productivity Slowdown, Measurement
Issues, and the Explosion of Computer Power. In W. C. Brainard,
& G. L. Perry, (Eds.), Brookings Papers on Economic Activity.
Washington, DC: The Brookings Institution, 1988.
Barua, A., Kriebel, C. and Mukhopadhyay, T. Information Technology
and Business Value: An Analytic and Empirical Investigation
. University of Texas at Austin Working Paper (May, 1991).
Belsey, D.A. Conditioning Diagnostics: Collinearity and Weak
Data in Regression. J. Wiley, New York, 1991.
Berndt, E. and Griliches, Z. Price Indexes for Microcomputers:
An Exploratory Study . National Bureau of Economic Research
Working Paper #3378 (1990).
Berndt, E. The Practice of Econometrics: classic and contemporary.
Reading, MA: Addison-Wesley, 1991.
Berndt, E.R. and Morrison, C.J. High-Tech Capital Formation and
Economic Performance in U.S. Manufacturing Industries: An Exploratory
Analysis. Journal of Econometrics, (1994, in press) .
Brooke, G.M. The Economics of Information Technology: Explaining
the Productivity Paradox. MIT Sloan School of Management CISR
Working Paper #238 (April, 1992).
Brynjolfsson, E. and Hitt, L. Is Information Systems Spending
Productive? New Evidence and New Results. International Conference
on Information Systems (Orlando, FL, 1993).
Brynjolfsson, E. The Productivity Paradox of Information Technology:
Review and Assessment. Communications of the ACM (1993,
in press).
Brynjolfsson, E., Malone, T., Gurbaxani, V., et al. Does Information
Technology Lead to Smaller Firms? Management Science,
Forthcoming
(1994).
Bureau of Economic Analysis, U.S.D.O.C. Fixed Reproducible
Tangible Wealth in the United States, 1925-85. Washington,
D.C.: U.S. Government Printing Office, 1987.
Council of Economic Advisors (Ed.), Economic Report of the
President. Washington, DC: United States Government Printing
Office, 1992.
David, P.A. Computer and Dynamo: The Modern Productivity Paradox
in a Not-Too-Distant Mirror. Stanford, CA, Center for Economic
Policy Research (1989).
Dos Santos, B.L., Peffers, K.G. and Mauer, D.C. The Impact of
Information Technology Investment Announcements on the Market
Value of the Firm. Information Systems Research, Vol. 4,
No. 1 (March 1993), pp. 1-23.
Dunne, T. Research and Development Expenditures and
Computer-Based
Technology Usage. University of Oklahoma Working Paper (October
1993).
Gordon, R.J. The Measurement of Durable Goods Prices. National
Bureau of Economic Research. Chicago: University of Chicago Press,
1993.
Gorman, J.A. Output Deflators by Industry. Raw data provided
on computer disk from Bureau of Economic Analysis (1992).
Griliches, Z. and Mairesse, J. Productivity and R&D at the
Firm Level. In Griliches, Z., (Ed.), R&D, Patents and
Productivity.
National Bureau of Economic Research. Chicago: University of Chicago
Press, 1984, pp. 339-374.
Griliches, Z. Issues in assessing the contribution of research
and development to productivity growth. Bell Journal of
Economics,
Vol. 10, No. 1 (1979), pp. 92-116.
Griliches, Z. The Search for R&D Spillovers. National
Bureau of Economic Research Working Paper #3768 (July, 1991).
Griliches, Z. Computers and Productivity: A Paradox of Substance
or Measurement . National Bureau of Economic Research Working
Paper (June, 1992).
Kambil, A., Henderson, J.C. and Mohsenzadeh, H. Strategic Management
of Information Technology Investments: An Options Perspective.
In R. D. Banker, R. J. Kauffman, & M. A. Mahmood, Strategic
Information Technology Management: Perspectives on Organizational
Growth and Competitive Advantage. Harrisburg, PA: Idea Group
Publishing, 1993.
Hall, B.H. New Evidence on the Impacts of Research and
Development.
University of California at Berkeley mimeo (May 19, 1993).
Hall, B.H. The Manufacturing Sector Master File: 1959-1987,
Documentation. National Bureau of Economic Research Working
Paper #3366 (April, 1990).
Harris, S.E. and Katz, J.L. Profitability and Information Technology
Capital Intensity in the Insurance Industry. In Proceedings
of the Twenty-First Hawaii International Conference on System
Science (1988)
International Data Corporation. U.S. Information Technology
Spending Patterns, 1969-1994. IDC Special Report #5368 (1991).
Kemerer, C.F. and Sosa, G.L. Systems Development Risks in Strategic
Information Systems. Information and Software Technology,
Vol. 33, No. 3, April (1991), pp. 212-223.
Kmenta, J. Elements of Econometrics. New York: Macmillan,
1986.
Krueger, A. How Computers Have Changed the Wage Structure:
Evidence from Microdata, 1984-1989 . National Bureau of Economic
Research Working Paper #3858 (October, 1991).
Lester, R.K. and McCabe, M.J. The Effect of Industrial Structure
on Learning by Doing in Nuclear Power Plant Performance. Rand
Journal of Economics, forthcoming (1993).
Loveman, G.W. An Assessment of the Productivity Impact on Information
Technologies. In T. J. Allen, & M. S. Scott Morton, Information
Technology and the Corporation of the 1990s: Research Studies.
MIT, 1994.
Mairesse, J. and Hall, B.H. R&D Investment and Productivity
Growth in the 1980s: A First Look at the United States and French
Manufacturing Sectors. Prepared for the AEA Meetings (Anaheim,
CA, 1993).
Maglitta, J. and Sullivan-Trainor, M. (Ed.), The Premier 100,
Computerworld, Framingham, Massachusetts: CW Publishing,
Inc., 1991.
Malone, T. and Rockart, J. Computers, Networks and the Corporation.
Scientific American, Vol. 265, No. 3 (1991), pp. 128-136.
Milgrom, P. and Roberts, J. The Economics of Modern Manufacturing:
Technology, Strategy, and Organization. American Economic Review,
Vol. 80, No. 3 (1990).
Morrison, C.J. and Berndt, E.R. Assessing the Productivity
of Information Technology Equipment in the U.S. Manufacturing
Industries. National Bureau of Economic Research Working Paper
#3582 (January 1990).
National Bureau of Economic Research. The Price Statistics
of the Federal Government. National Bureau of Economic Research.
New York: Columbia University Press, 1961.
Pelaia, E. "IBM Terminal Prices". (1993) IBM
Representative, personal communication.
Popkin, J., and Company. The Impact of Measurement and Analytical
Issues in Assessing Industry Productivity and its Relation to
Computer Investment . Mimeo, Washington, DC (October 1992).
Quinn, M.A., Craumer, M.A., Weaver, A., et al. Critical Issues
of Information Systems Management for 1993. The Sixth Annual
Survey of Information Systems Management Issues. Cambridge
MA: CSC Index, 1993.
Roach, Stephen S. America's Technology Dilemma: A Profile of
the Information Economy. Special Economic Study, Morgan Stanley
(April 1987).
Scott Morton, M. (Ed.). The Corporation of the 1990s: Information
Technology and Organizational Transformation. New York: Oxford
University Press, 1991.
Siegel, D. and Griliches, Z. Purchased Services, Outsourcing,
Computers and Productivity in Manufacturing. National Bureau
of Economic Research Working Paper #3678 (April, 1991).
Simon, Herbert A. On the Behavioral and Rational Foundations of
Economic Dynamics. Journal of Economic Behavior and
Organizations,
Vol. 5, (1984), pp. 35-66.
Strassmann, P.A. The Business Value of Computers. Information
Economics Press, New Canaan, Conn, 1990.
Thurow, L. Are Investments in Information Systems Paying Off?
(interview). MIT Management (1990).
Varian, H. Microeconomic Analysis. W. W. Norton &
Company,
Inc., New York, 1992.
Weill, P. The Relationship Between Investment in Information Technology
and Firm Performance: A Study of the Valve Manufacturing Sector.
Information Systems Research, Vol. 3, No. 4 (December 1992).
Wilson, D. Assessing the Impact of Information Technology on
Organizational
Performance. In R. Banker, R. Kauffman, & M. A. Mahmood,
Strategic
Information Technology Managementt. Harrisburg, PA: Idea Group,
1993.
[2]However, output and GDP are not directly comparable because GDP is net of interfirm purchases. On a comparable basis (Value-Added), our sample represents approximately 13% of the US economy in 1991.
[3] Specifically, the "management productivity of information technology" (MPIT) dataset, which surveyed 60 business units of 20 participating firms for the period 1978-1982.
[4] The precise definition of "IT" varies from study to study. Morrison and Berndt included scientific instruments, communications equipment, photocopiers and other office equipment as well as computers in their definition. Others define IT even more broadly, including software, services and related peripheral equipment. As described in section 2.3 below, the definition used in our study is fairly narrow and includes separate estimates for the effect of corporate computer capital and corporate IS labor.
[5] As the National Bureau of Economic Research (1961) put it: "If a poll were taken of professional economists and statisticians, they would designate the failure of price indexes to take full account of quality changes as the most important defect in these indexes." No good methodology exists for incorporating some of the other benefits, such as variety. Baily and Gordon (1988) estimate that "true" annual productivity growth might be as much as 0.5% higher overall than reported in official statistics.
[6] (Berndt, 1991) lists over a hundred references on this approach and presents an excellent literature review.
[7] Another common way to operationalize the theory is to use the production function to derive a "cost function" which provides the minimum cost required for a given level of output. While cost functions have some attractive features, they require access to firm-level price information for each input, which are data we do not have.
[8] A more complete model might include, in addition to these controls, other variables which may affect output such as the organization's maturity in the use of IT or the degree of restructuring it has undergone. We hope to explore such models in future research.
[9] For instance, a simple linear relationship between inputs and outputs is ruled out by these constraints. A linear production function implies that a firm will either use only the lowest cost input, or an indeterminate mix of all inputs if the prices are exactly the same.
[10] For instance, Hall (1993) introduces her Cobb-Douglas production function with the words: "...using the by now standard growth accounting framework...".
[11] Formally, the output elasticity of computers, EC, is defined as: . For our production function, F, this reduces to: . The ROI for computers is simply the output elasticity multiplied by the ratio of output to computer input:
[12]For expositional simplicity, we write this equation with a single intercept [[beta]]0. In the actual analysis, this intercept is allowed to vary by year and industry or by year and sector.
[13] Sometimes also called IZEF, the iterated version of Zellner's efficient estimator, ISUR yields estimates that are numerically equivalent to the maximum likelihood estimator (Berndt, 1991). The ISUR procedure starts by estimating the coefficients by OLS to obtain an initial estimate of the error term covariance matrix, and then iteratively refines this estimate until convergence is reached at minimum error. This procedure implicitly corrects for serial correlation among the variables even when there are missing observations for some firms in some years. More traditional methods of correcting for serial correlation in panel data sets (Kmenta, 1986) require complete data and do not seem to perform well with short time dimensions.
[14]Specifically, the survey targets Fortune 500 manufacturing and Fortune 500 service firms that are in the top half of their industry by sales (see Table 2a).
[15]Compustat II provides financial and other related information for publicly traded firms, primarily obtained through annual reports and regulatory filings.
[16] Specifically, we estimated a figure for the value of terminals and the value of PCs and then weighted them by the proportion of PCs versus terminals. For terminals, the we estimated the value as the average list price of an IBM 3151 terminal in 1989 which is $609 (Pelaia, 1993). For PCs we used the average nominal PC cost over 1989-1991 of $4,447, as reported in Berndt & Griliches (1990). These figures were then weighted by the proportion of PCs to terminals in the 1993 IDG survey (58% terminals). The resulting estimate was .42*$609 + .58* $4,447 = $2,835.
[17]An alternative measure of capital stock was computed by converting historical capital investment data into a capital stock using the Winfrey S-3 table. This approach was used in earlier versions of this paper (Brynjolfsson & Hitt, 1993). However, the calculation shown above is more consistent with previous research (see e.g. (Hall, 1993)).
[18] For instance, the custom of treating checking accounts as "outputs" and interest bearing accounts as inputs was undermined when interest-bearing checking accounts were introduced.
[19] The impact of these changes in both cases was to lower the return to COMPUTER CAPITAL as compared to the results on the full sample.
[20] As noted in footnote 11, supra, , which in this case is .0169/.0209 = .8086 or about 81%.
[21] It is worth noting that our approach provides estimates of the marginal ROI of each input: how much the last dollar of stock or flow added to output. In general, infra-marginal investments have higher rates of return than marginal investments, so the return to the first dollar invested in computers is likely to be even higher than the marginal returns we reported.
[22] We thank Dan Sichel for pointing this out.
[23] Technically, "negative capital gains" may be a more accurate term than "depreciation", since computer equipment is more likely to be replaced because of the arrival of cheaper, faster alternatives than because it simply wears out.
[24] As discussed in section 2, it is also possible that there are other "hidden" expenses associated with COMPUTER CAPITAL in addition to depreciation. On the other hand, firms invest in IT at least partly to move down the learning curve (Brynjolfsson, 1993) or create options (Kambil, Henderson & Mohsenzadeh, 1993), and these effects may create "assets" as large as those lost to depreciation. The high gross returns to computer capital suggest that even if there were significant additional expenses associated with COMPUTER CAPITAL, its net returns would still be positive.
[25] A decline in the returns to COMPUTER CAPITAL between 1989 and 1990 is also evident in a balanced panel of 201 firms in the sample for 1989-1991.
[26] Note that if we had used OLS, further assumptions would be required: that all error terms are independent and constant variance over time.
[27] We were unable to do the White test for heteroskedasticity on these data because of limitations of our econometric software, and the large number of regressors.
[28] This is not the case if an input variable is systematically understated by a constant multiplicative factor. In this case, the coefficient estimates would be unchanged.
[29] However, in the presence of individual firm effects, lagged values are not valid instruments. While we did not test for firm effects, we suspect they may be important, and so the results of our 2SLS estimates should be interpreted with caution.
[30]The translog is a second order approximation to an arbitrary production function and contains for each input, the value of the input, the value of the input squared and all multiplicative interaction terms between the input and all other inputs. The Cobb-Douglas production function is a special case of the translog with the square and interaction terms restricted to be zero. For four factors of production, the full translog requires that 14 coefficients be estimated (not including intercepts).
[31]The elasticity for computer capital can be calculated for the "average" firm in the sample by taking the partial derivative of output with respect to COMPUTER CAPITAL for the translog specification, and substituting the appropriate coefficient estimates and average factor input values.
[32] Multicollinearity diagnostics (Belsey, 1991) also indicated that most of the added terms in the translog were highly collinear, which could account for the higher standard errors.
[33] This is because multiplicative scaling of a regressor in a logarithmic specification will not change the coefficient estimate or the standard error. All the influence of the multiplier will appear in the intercept term which is not crucial to our analysis.
[34] The MIT Center for Coordination Science and International Financial Services Research Center jointly sponsored a Workshop on IT and Productivity which was held in December, 1992.